２次方程式

 因数分解の話も終了して２次方程式中心の話になります。２次方程式を簡単に解くための手段として因数分解を今まで習ってきたわけですが、 因数分解できない２次方程式も多く存在します。


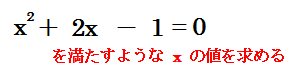　　＜平方完成の画像が表示されていません！＞　　 　 x2+2x-1=0 を解きなさい。

 この式を因数分解しようとしてみても、２つの数を掛けて「-1」、足して「+2」になるような 値というのは見つかりません。
よって「解なし」・・・が答えかと言うと、そういうわけではありません。ここで登場するのが「平方完成」と呼ばれる技術です。なんのこっちゃ分からない・・・と 感じるかと思いますが、とりあえず次の説明を読んで下さい。
知っているという方は「解の公式」を自力で作ることができますでしょうか？これが出来ないのであればきちんと読んで下さい。


 平方完成における第一ステップはx2・xの項をまとめて(x + …)2の形にすることです。
言いかえれば、
   ax2+bx+c = 0 を
   a(x + d)2+e = 0
という形に変形する、ということです。
 どうやるの？という話ですが、先程の問題 x2+2x-1=0 の場合 x2+2x の部分に着目して、これを２乗の形にまとめましょう。
x2+2x を無理やり２乗の形にすると (x + 1)2-1 という形にまとめられます。
    x2+2x　=　(x + 1)2-1

　 平方完成：コツ　  このときのコツとしましては　xの項の係数の半分の値を(x + …)2 の…に代入すること　です。
そして定数項（xを含まない項）については帳尻を合わせよう（右辺と左辺が一致するようにしよう）という意識で設定してあげて下さい。 いくつか例をあげますと、
    x2+8x  =　(x + 4)2-16
    x2-8x  =　(x - 4)2-16
    x2+10x =　(x + 5)2-25
    x2-9x  =　(x - 9/2)2-81/4
    x2+x   =　(x + 1/2)2-1/4
となるということです。


 以上の話から 先程の問題 x2+2x-1 = 0 については
    x2+2x-1 = 0
    ∴(x + 1)2-2 = 0
    ∴(x + 1)2 = 2
と変形できます。そしてこの式の両辺の平方根を取ることで
    ∴x + 1 = ±√2
となります。

　 「±」ってなに？？　   ± という記号が今登場しましたが、この記号は以降度々使うことになります。
意味としてはプラスとマイナス両方どちらもという意味です。
    (x + 1)2 = 2 ・・・（※）
の式の (x + 1) がどのような値だったら２乗して２になるか？と考えてみて下さい。
(x + 1) が +√2 のとき確かに（※）の 式を満たしますが
(x + 1) が -√2 のときも確かに（※）を満たしますね？

よって
    (x + 1)2 = 2
    ∴x + 1 = ±√2　　(√2または-√2)
と変形できます。


さらに式を整理すれば
    x2+2x-1 = 0
    ∴(x + 1)2-2 = 0
    ∴(x + 1)2 = 2
    ∴x + 1 = ±√2
    ∴x = - 1 ± √2 (- 1 + √2　または　- 1 - √2)
となり答えが求められました。２次方程式の解は通常２つの解が出てきます。
今回の場合 - 1 + √2　と　- 1 - √2が解というわけですね。


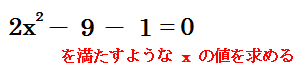　　＜平方完成の画像が表示されていません！＞　　 　 2x2-9x-1=0 を解きなさい。

 先程と違い今度はx2の係数が１ではありません。
この時に重要なのは先程も言ったように平方完成では
   ax2+bx+c = 0 を
   a(x + d)2+e = 0
という形に変形する、ということです。
(ax + d)2+e = 0などとaの値を（・・・・）カッコの中に入れないように注意して下さい。


 それでは 2x2 - 9x の部分に着目して２乗の形にまとめましょう。そこでまずは x2の係数2に着目して式全体をまとめます。すると
    2x2 - 9x = 2(x2 - 9/2x)
と出来ます。ここから先は先程と同様です。xの係数が9/2と分数になっていますが、 気にせずに進めるだけです。
    2x2 - 9x = 2(x2 - 9/2x)
        = 2{(x - 9/4)2 - 81/16}
        = 2(x - 9/4)2 - 81/8

　 平方完成：コツ　  このときのコツとしましては　xの項の係数の半分の値をさらにaで割ったものをa(x + …)2 の…に代入すること　です。
そして定数項（xを含まない項）については帳尻を合わせよう（右辺と左辺が一致するようにしよう）という意識で設定してあげて下さい。 いくつか例をあげますと、
    3x2 + 8x =　3(x + 4/3)2 - 16/3
    5x2 - 8x =　5(x - 4/5)2 - 16/5
    2x2 + 10x =　2(x + 5/2)2 - 25/2
    7x2 - 9x =　7(x - 9/14)2 - 81/14
    2x2 + 4x =　2(x + 1)2 - 2
となるということです。


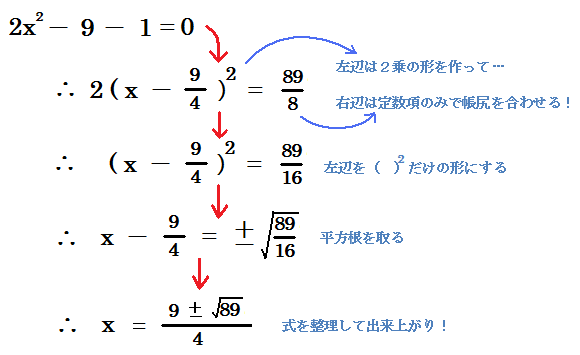
　　＜平方完成の画像が表示されていません！＞　　
 後は前回と同様に式変形をしたら終わりです。先程の問題 2x2-9x-1 = 0 については
    2x2-9x-1 = 0
    ∴2(x - 9/4)2 -81/8 -1 = 0
    ∴2(x - 9/4)2 = 89/8
    ∴(x - 9/4)2 = 89/16
と変形できます。そしてこの式の両辺の平方根を取ることで
    ∴x - 9/4 = ±√89 / √16
    ∴x - 9/4 = ±√89 / 4
    ∴x = 9/4 ± √89 / 4
が答えになります。



 このように√等の記号が入って一見汚くも見えますが、どのような問題であってもこれで２次方程式の解を求める事が出来るのです。
さて、あとは例のごとく練習あるのみです。下に問題を用意しましたので、ガツガツ解いて実践力を養いましょう。

　 平方完成：例題　
　　　 x2-10x+3 = 0の解を求めなさい。

　 x2-10x+3 = 0
　∴　(x - 5)2 = 22   (両辺の定数項を合わせると元の "3" になるように右辺を定めるのがコツ)
　∴　x - 5 = ± √22
　∴　x = 5 ± √22


　　　 x2+5x+3 = 0の解を求めなさい。

　 x2+5x+3 = 0
　∴　(x + 5/2)2 = 13/4   (両辺の定数項を合わせると元の "3" になるように右辺を定めるのがコツ)
　∴　x + 5/2 = ± √13 / √4
　∴　x = - 5/2 ± √13 / 2


　　　 4x2+8x+1 = 0の解を求めなさい。

　 4x2+8x+1 = 0
　∴　4(x + 1)2 = 3   (両辺の定数項を合わせると元の "1" になるように右辺を定めるのがコツ)
　∴　(x + 1)2 = 3/4
　∴　x + 1 = ± √3 / √4
　∴　x = - 1 ± √3 / 2


　　　 7x2+8x+1 = 0の解を求めなさい。

　 7x2+8x+1 = 0
　∴　7(x + 4/7)2 = 9/7   (両辺の定数項を合わせると元の "1" になるように右辺を定めるのがコツ)
　∴　(x + 4/7)2 = 9/49
　∴　x + 4/7 = ± √9 / √49
　∴　x + 4/7 = ± 3/7
　∴　x = - 4/7 ± 3/7  (すなわち、x = - 1 , - 1/7)

　　　　　　別解　(因数分解でも解ける)
　 7x2+8x+1 = 0
　　∴ (x + 1)(7x + 1) =0
　　∴ x = -1 , - 1/7   因数分解出来るときはした方が圧倒的に早い！


　　　 x2-18x+81 = 0の解を求めなさい。

　 x2-18x+81 = 0
　∴　(x - 9)2 = 0
　∴　x - 9 = 0   右辺が "0" なので答えは一つだけになる。
　∴　x = 9


　　　 x2-2x+3 = 0の解を求めなさい。

　 x2-2x+3 = 0
　∴　(x - 1)2 = - 2
　∴　解なし
   今までは右辺が正であったため平方根を取ることが出来たが、今回は負。
   よって平方根を取ることが出来ないため「このようなxは存在しない」ということになる。


 どうでしょうか？平方完成に慣れてきましたでしょうか？まず因数分解が出来るときはしてしまいましょう。その方が圧倒的に早いので。
最後の問題などは意地悪な問題ですが、２次方程式の解がないということはよくある話です。この機会に知っておきましょう。

 しかし、今までに習ってきた因数分解に比べ手順などが色々面倒で計算量も無駄に多いなぁ…と感じた方もいるかと思います。その感覚は正しいです。 出来ることなら因数分解で解きたい！という意識を持っておくようにしましょう。