練習問題（応用編）│斜交座標を用いて平面幾何を解く

 前ページに引き続き、斜交座標の問題ですが、今までとは少し違う形の図形を扱います。

---

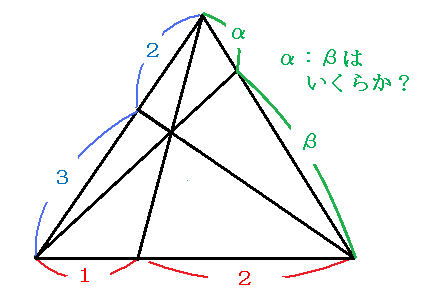
　 右図で示された α:βの比 を求めなさい。

---

　　　　斜交座標を使って解く

　今までのようなメネラウスの定理で見るような、三角形２つが重なったような形とは少し違います。 この問題を以前に扱ったようなベクトルを用いて平面幾何を解く手法でやろうとすると 大変な労力がかかります。「ベクトルaとベクトルbを置いて...」と考えただけでも大変なのは見て取れます。
そこで今回も使うのは斜交座標です。見た目が変わってますが基本的には座標においてしまえばとても簡単な話なのです。まずは下の解答例を見ずに自力で解いてみましょう。

難しそうだ・・・という方は”斜交座標のうちどの点を(1,0)と(0,1)の規定に考えれば良いか”ということについてだけでも、考えて見ましょう。

　 斜交座標を用いて解く（解答）　

　　右図のように点Ｏ,Ａ~Ｆを定める。
　ここでＯを原点としＯＡ，ＯＢを規定とする斜交座標系ＸＹを用意しＡ（1,0）,Ｂ（0,1）と定める。
　この時,比の関係からＣ（1/3,0）,Ｄ（0,3/5）と定める事が出来る。






　　すると
　   直線AB:X + Y = 1
　   直線AD:X + 5/3 Y = 1
　   直線BC:3X + Y = 1
　という直線の式が得られ、このうち２直線ADとBCの交点がＥであるためこれを解いて
　   E( 1/6 , 1/2 )
　と求める事が出来る。






　　今Ｆは直線ＯＥと直線ＡＢの交点であるので直線ＯＥの式を求めたい。
　　すると
　   直線OE:Y = 3X
　という直線の式が得られる。






　　すると
　   直線AB:X + Y = 1
　   直線OE:Y = 3X
　という直線の式より、２直線ABとOEの交点がＦであるためこれを解いて
　   F( 1/4 , 3/4 )
　と求める事が出来る。






　　以上を踏まえると、　α：β　については
　   　α：β　= 1/4:3/4
　       = 1:3

　どうでしょうか？座標の計算をするだけで非常に簡単に、スムーズに解くことが出来ました。
大抵の平面幾何の「比の問題」などではこの斜交座標の考え方を活かせることが多いです。一度座標の設定さえ出来てしまえば もうあとは簡単です。内容としては中学２年生レベルの直線の式の問題を解くだけで終わりです。
ぜひ斜交座標の考え方を身につけて応用問題でも取り組めるようにしましょう。