数列

 さて、これまでは等差数列について触れてきましたが、ここからは等比数列というものに 触れていきます。
等比数列は今までのページでも若干触れてきましたが、以下のような数列になります。
  等比数列： ３，６，１２，２４，４８，９６，１９２，・・・
要するに一定の倍率を掛けていく、という数列ですね。ここでは２倍していく数列ということになります。
ここで掛けていく一定の倍率のことを公比と呼び、ここでは上の数列の場合ですと初項が３・公比が２の 数列ということになります。
それではこの等比数列についてanを用いた一般の形のものについて触れていきましょう。


突然ですが
「an = 3×2n-1 」についてみるならば
n = 1,2,3,4,5...　と代入することによって，それぞれ数列の１番目,２番目,３番目,４番目,５番目・・・の値を求めることができます。

すなわちan = 3×2n-1とは
  n = 1　（数列の１番目）：a1=3×21-1 = 3
  n = 2　（数列の２番目）：a2=3×22-1 = 6
  n = 3　（数列の３番目）：a3=3×23-1 = 12
  n = 4　（数列の４番目）：a4=3×24-1 = 24
  n = 5　（数列の５番目）：a5=3×25-1 = 48
・・・となるような数列を表現しています。

「・・・あれ？」と思われた方もいると思いますが、要するにこの数列はこのページの上に書いた数列と同じです。

  等比数列： ３，６，１２，２４，４８，９６，１９２，・・・
すなわち初項が３・公比が２の等比数列ということになります。


さらに練習として次の数列について見てみます。
先ほどが「an = 3×2n-1 」だったのに対して 「an = 5×2n-1 」についてみるならば
n = 1,2,3,4,5...　と代入することによって、それぞれ数列の１番目,２番目,３番目,４番目,５番目・・・の値を求めることができます。

すなわちan = 5×2n-1とは
  n = 1　（数列の１番目）：a1=5×21-1 = 5
  n = 2　（数列の２番目）：a2=5×22-1 = 10
  n = 3　（数列の３番目）：a3=5×23-1 = 20
  n = 4　（数列の４番目）：a4=5×24-1 = 40
  n = 5　（数列の５番目）：a5=5×25-1 = 80
・・・となるような数列を表現しています。

  等比数列： ５，１０，２０，４０，８０，１６０，３２０，・・・
すなわち初項が５・公比が２の等比数列ということになります。


さらに練習として次の数列について見てみます。
先ほどが「an = 3×2n-1 」や「an = 5×2n-1 」だったのに対して 「an = 2n 」についてみるならば
n = 1,2,3,4,5...　と代入することによって、それぞれ数列の１番目,２番目,３番目,４番目,５番目・・・の値を求めることができます。

すなわちan = 2nとは
  n = 1　（数列の１番目）：a1=21 = 2
  n = 2　（数列の２番目）：a2=22 = 4
  n = 3　（数列の３番目）：a3=23 = 8
  n = 4　（数列の４番目）：a4=24 = 16
  n = 5　（数列の５番目）：a5=25 = 32
・・・となるような数列を表現しています。

  等比数列： ２，４，８，１６，３２，６４，１２８，・・・
すなわち初項が２・公比が２の等比数列ということになります。



・・・ここまでの流れで分かったでしょうか？すなわち
  an = 3×2n-1　・・・　初項が３・公比が２の等比数列
  an = 5×2n-1　・・・　初項が５・公比が２の等比数列
  an = 2n = 2×2n-1　・・・　初項が２・公比が２の等比数列
となっている，ということです．この３つはどれも等比数列です。

さらにどうにも数列の中の「2n-1」の中に含まれている「2」によって公比が決定しており、
数列の中の「2n-1」の前に付いている数によって初項が決定しているように見受けられますね。

さらに同様に計算すれば分かるのですが
  an = 3n = 3×3n-1　・・・　初項が３・公比が３の等比数列
  an = 5×3n-1　・・・　初項が５・公比が３の等比数列
  an = 2×3n-1　・・・　初項が２・公比が３の等比数列
となりますし
  an = 3×5n-1　・・・　初項が３・公比が５の等比数列
  an = 5n = 5×5n-1　・・・　初項が５・公比が５の等比数列
  an = 2×5n-1　・・・　初項が２・公比が５の等比数列
となります。


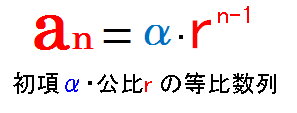　　＜数列の画像が表示されていません！＞　　  勘の良い方はもう気が付いたかもしれませんが、一般に
  「an = α・rn-1 」
という形で表される数列というのは
  「初項αで公比rの等比数列」
となります。


何やらrn-1の中にn-1と不思議な数が入っていますが、このような値が入っていることは 等差数列の公式と初項を勉強したときと似ています。
要するにn=1を代入したときに初項がαになるように調整しているだけです。

実際に「an = α・rn-1 」に代入してみると一目瞭然ですが
  n = 1　（数列の１番目）：a1=α・r1-1 = α
となるため、αやrがどのような値であったとしても、n-1という形をしているおかげで初項「a1」は必ずαとなります。


　　＜数列の画像が表示されていません！＞　　  しかし「少しこの形は面倒だなあ」と思われる方は「an = α・rn 」の形があれば等比数列だと 思っても大丈夫です。等比数列の最大の特徴はとにかく「an」の式の中にrnのようにnを指数に持つ部分をもつことです。
この時にn乗される値が公比になると覚えておけば問題ありません。

初項は何か・・・という話ですが、どんな数列でもそうですが初項はn=1を代入すればOKです。これはすぐに求められますね？（笑）


以下は練習問題になります。

　 等比数列　
　　　 「an = 7×2n-1：nは1以上」の数列について初項から順に5つ答え、初項と公比を答えなさい．

  ７，１４，２８，５６，１１２，・・・
  初項：７  公比：２


　　　 「an = 7×1n-1：nは1以上」の数列について初項から順に5つ答え、初項と公比を答えなさい．

  ７，７，７，７，７，・・・
  初項：７  公比：１


　　　 「an = (-3)×2n：nは1以上」の数列について初項から順に5つ答え、初項と公比を答えなさい．

  -６，-１２，-２４，-４８，-９６，・・・
  初項：-６  公比：２


　　　 「an = 7×(-3)n-1：nは1以上」の数列について初項から順に5つ答え、初項と公比を答えなさい．

  ７，-２１，６３，-１８９，５６７，・・・
  初項：７  公比：-３


　　　 「an = 9×(-1)n：nは1以上」の数列について初項から順に5つ答え、初項と公比を答えなさい．

  -９，９，-９，９，-９，・・・
  初項：-９  公比：-１


　　　 「an = 48×(1/2)n：nは1以上」の数列について初項から順に5つ答え、初項と公比を答えなさい．

  ２４，１２，６，３，３/２，・・・
  初項：２４  公比：１/２


　　　 「an = 3n-3：nは1以上」の数列について初項から順に5つ答え、初項と公比を答えなさい．

  １/９，１/３，１，３，９，・・・
  初項：１/９  公比：３



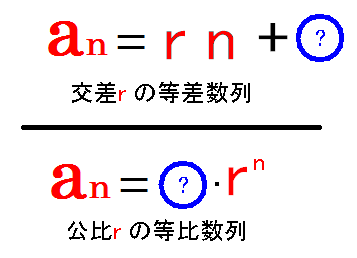　　＜数列の画像が表示されていません！＞　　  簡単に等差数列と等比数列の式の形を比較すると右図のようになります。

要するに
「an」がr・nの形を含んでいれば公差rの等差数列
「an」がrnの形を含んでいれば公比rの等比数列
となります。

等比数列と等差数列の式の形は簡略に理解できるようになりましたでしょうか？