数列
一応教科書に則って・・・ということで等差数列の公式について軽く触れておきます。
教科書などに載っている公式は次のようになります。
「an = (公差)×(n-1) + (初項) 」
さらに(公差)をr、(初項)をa1と書けば
「an = r(n-1) + a1 」
と書くこともできます。
ここでいう(公差)とは等差数列が一定の割合で増えていくわけですが、その割合のことを示し、(初項)とは数列の最初の値のことです。
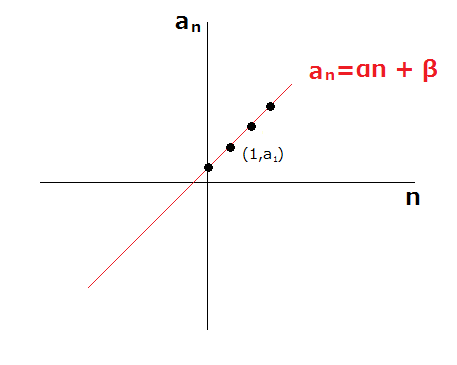
しかし、ここでいう公式は至極当然のことではあります。なにやら (n-1) などと不思議な数が出てきますが、要するに
n=1のときにa1となるようにしただけです。
前ページのようにグラフで考えれば当然であることが分かるかと思います。
しかしどうでしょうか?以前に述べたような
「an = αn + β 」
という式で書いた方が見た目は少なくとも綺麗です。
βはy切片であることを覚えておけば出来るはずです。
公式の方が分かりやすい場合はそれでも良いのですが、あまり公式に惑わされないようにしてください。
nの係数は公差なのですぐに分かるかと思うのですが、定数項については少し計算が必要になります。
ここでの解き方は普段どのようにして直線の式を求めているかに近いと思います。
例えば
交差が4で、a4=5となるような数列は?という問題と
傾きが4で、(4,5)を通る直線の式は?という問題は本質的には同等です。
ここでの直線の式を求めるときの頭の動かし方と同じように等差数列の式を作れば十分です。新しく公式を覚える必要はありません。
以下は練習問題になります。
以上で等差数列も終了となります。計算手法もつかめましたでしょうか?
基本的には直線の計算をしていた時と頭の動かし方は同じなので、それさえ理解できればスムーズに理解できるはずです。
