数列
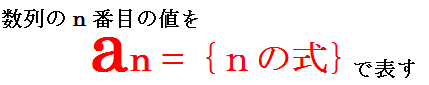それではおそらく高校数学で最も使う数列の標準形{an}を用いたnの式で表すことを
行っていきましょう．
数列の最初のページでも若干紹介しましたが{an}とは数列のn番目を数のことを指し
an = 2n - 1
などといった形で表現します．
練習として
「an = 2n - 1 」についてみるならば
n = 1,2,3,4,5... と代入することによって，それぞれ数列の１番目,２番目,３番目,４番目,５番目・・・の値を求めることができます
すなわちan = 2n - 1とは
n = 1 （数列の１番目）：a1=2×1 - 1 = 1
n = 2 （数列の２番目）：a2=2×2 - 1 = 3
n = 3 （数列の３番目）：a3=2×3 - 1 = 5
n = 4 （数列の４番目）：a4=2×4 - 1 = 7
n = 5 （数列の５番目）：a5=2×5 - 1 = 9
・・・となるような数列を表現しています．
もうこれがどのような数列なのか分かったでしょうか？前ページで触れたような数列を順番に列挙する手法で書けば
１，３，５，７，９，１１，１３，１５，１７，・・・
という数列になります．要するに奇数です．
別の言い方をすれば２ずつ増える数列(等差数列)となります．
さらに練習として次の数列について見てみます．
さきほどが「an = 2n - 1 」だったのに対して 「an = 3n - 1 」についてみるならば
n = 1,2,3,4,5... と代入することによって，それぞれ数列の１番目,２番目,３番目,４番目,５番目・・・の値を求めることができます
すなわちan = 3n - 1とは
n = 1 （数列の１番目）：a1=3×1 - 1 = 2
n = 2 （数列の２番目）：a2=3×2 - 1 = 5
n = 3 （数列の３番目）：a3=3×3 - 1 = 8
n = 4 （数列の４番目）：a4=3×4 - 1 = 11
n = 5 （数列の５番目）：a5=3×5 - 1 = 14
・・・となるような数列を表現しています．
これも数列を順番に列挙する手法で書けば
２，５，８，１１，１４，１７，２０，２３，２６，・・・
という数列になります．別の言い方をすれば３ずつ増える数列(等差数列)となります．
さらに練習として次の数列について見てみます．
さきほどが「an = 2n - 1 」や「an = 3n - 1 」だったのに対して 「an = 4n - 1 」についてみるならば
n = 1,2,3,4,5... と代入することによって，それぞれ数列の１番目,２番目,３番目,４番目,５番目・・・の値を求めることができます
すなわちan = 4n - 1とは
n = 1 （数列の１番目）：a1=4×1 - 1 = 3
n = 2 （数列の２番目）：a2=4×2 - 1 = 7
n = 3 （数列の３番目）：a3=4×3 - 1 = 11
n = 4 （数列の４番目）：a4=4×4 - 1 = 15
n = 5 （数列の５番目）：a5=4×5 - 1 = 19
・・・となるような数列を表現しています．
これも数列を順番に列挙する手法で書けば
３，７，１１，１５，１９，２３，２７，３１，３５，・・・
という数列になります．別の言い方をすれば４ずつ増える数列(等差数列)となります．
・・・ここまでの流れで分かったでしょうか？すなわち
an = 2n - 1 ・・・ ２ずつ増える数列(等差数列)
an = 3n - 1 ・・・ ３ずつ増える数列(等差数列)
an = 4n - 1 ・・・ ４ずつ増える数列(等差数列)
となっている，ということです．この３つはどれも等差数列です．
さらにどうにも数列の中の「n」の前についている係数によって等差数列の増加率が決定しているように見受けられますね．
さらに同様に計算すれば分かるのですが
an = 2n + 3 ・・・ ２ずつ増える数列(等差数列)
an = 3n + 3 ・・・ ３ずつ増える数列(等差数列)
an = 4n + 3 ・・・ ４ずつ増える数列(等差数列)
となります．
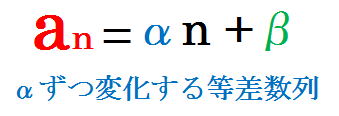勘の良い方はもう気が付いたかもしれませんが，一般に「an = αn + β 」
という形で表される数列というのはαずつ変化する等差数列となります．
どうしてもコレがしっくりこない方は
nが１つ大きくなるとanはα大きくなるのだから当たり前！ とイメージしても良いです．αは変化率を意味しているというのを意識しましょう．
「・・・アレ？じゃあβは何を意味しているの？」を思われる方もいると思うので，ここでn=0となる数列の０番目（考えないことが多いですが）を含めて考えましょう．
０番目(n=0)も含めて先程の３つの数列を列挙してみると
an = 2n - １ ＝＞ - １，１，３，５，７，９，１１，・・・
an = 3n - １ ＝＞ - １，２，５，８，１１，１４，１７，・・・
an = 4n - １ ＝＞ - １，３，７，１１，１５，１９，２３，・・・
※n=0,1,2,3,4,5,6 まで代入してみました
となります．
さらに同様に次のような数列も考えてみましょう．
an = 2n + ３ ＝＞ ３，５，７，９，１１，１３，１５，・・・
an = 3n + ３ ＝＞ ３，６，９，１２，１５，１８，２１，・・・
an = 4n + ３ ＝＞ ３，７，１１，１５，１９，２３，２７，・・・
※n=0,1,2,3,4,5,6 まで代入してみました
となります．
大凡の性質に気がついたでしょうか？実はβは数列にn=0を代入したときの値（数列の０番目）に相当するのです．
別の言い方をするならばβとはa0に相当するということです．
しかし一般的には数列{an}とはnが１以上において定義することが多いです． ここでは数列の０番目などと特殊な表現をしましたが，そんなに登場するものではないのが実際のところです．
以下は練習問題になります。