数列
前ページでは新しく数列の和という分野に入り、Σという記号の
表記方法について学んできました。
しかし、計算方法にはこれといった工夫をすることなく地道に解いてきたわけですが数が増えてくると、これは大変になってきます。
例えば

などという計算はどうみても大変そうです。単純に考えれば
1+2+3+...
と計算する以外に思いつかないかもしれませんが、これを上手く簡単に解く方法というのがガウスによって、当時10歳だった時に編み出されました。
数列には等差数列や等比数列などがありますが、ここではその中でも等差数列に着目して、その和を求める手法について学んでいきます。
1から20までの自然数の和を求めなさい
いきなり1から100まで求めるわけにもいかないので、まずは20までにします。
何をしたらいいのか・・・ということなのですが、とりあえず良く分からないのでまずは式を書いてみます。
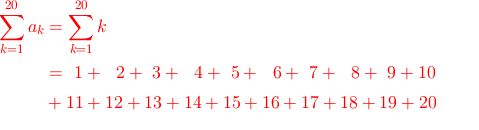
とりあえず書いてみました。
しかし、このまま計算していては今までの単純な計算方法と変わりません。そこで次のように並べ替えることにします。
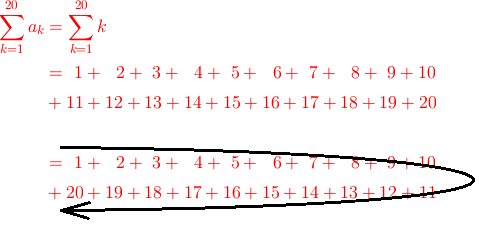
1から10までと11から20までで分けて、途中で折り返すように並べてみました。
何か見えてきましたでしょうか?
さらに次のように縦に並んだ数字同士を足し算します。
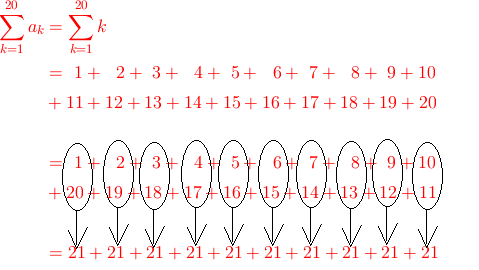
なんと足し算した結果がすべて同じになりました!
これはかなり強力なことです。
なぜならこの結果を使えば、次のように掛け算によって計算できるからです。
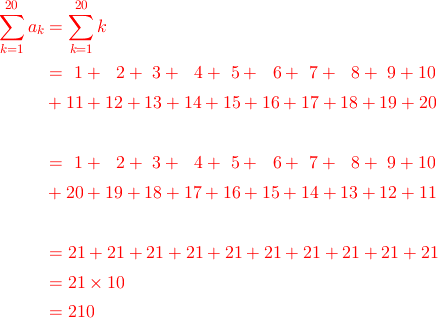
途中で並べ替えたりしただけで、実質的な計算をしたのは最後の21×10という計算だけです。
計算手法を述べると
「 (最初の数+最後の数)×(全体の個数)÷2 」
となります。非常に簡単ですね。「最初の数と最後の数の平均に全体の個数を掛ける」というイメージでもいいです。
「・・・でもマグレじゃないの?」なんて思う方もいるかもしれませんが、じつは
すべての等差数列でこのような計算方法が成立します!!!
等差数列の性質上、「差が均一」ですので途中で縦に並んだ数字同士を足し合わせると必ず一致するのです。
「いや・・・でも今は20個の足し算だったわけだよね?つまり偶数だったわけだけど、奇数だとダメじゃない?」
と思った人もいることでしょう。それでは数をもう一つ付け加えます。
1から21までの自然数の和を求めなさい
この場合はどうなるでしょうか?全体の個数が奇数になりました。
しかしそれは下のように考えてください。
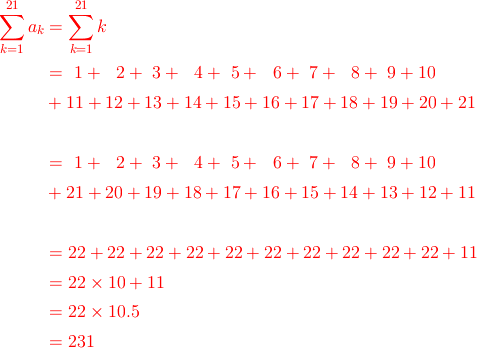
結局同じです。折り返し地点の「11」だけが一人ぼっちという形になりますが、計算手法は概して変わりません。
やはり
「 (最初の数+最後の数)×(全体の個数)÷2 」
となります。先ほどと同じで「最初の数と最後の数の平均に全体の個数を掛ける」というイメージでもいいです。
では、もう少し複雑な等差数列の場合はどうなるのでしょうか?
ak=3k-1の数列においてk=1から21までの和を求めなさい
この場合はどうなるでしょうか?同じように計算してみましょう。
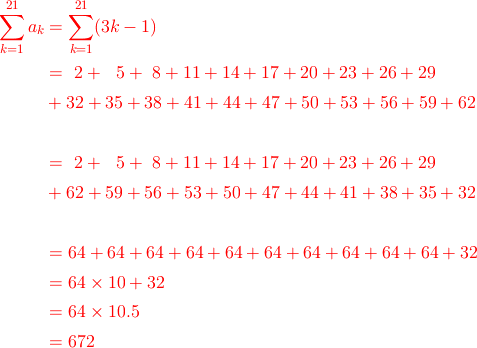
やはり同じ結果になりました。
「 (最初の数+最後の数)×(全体の個数)÷2 」
となります。先ほどと同じで「最初の数と最後の数の平均に全体の個数を掛ける」というイメージでもいいです。
実は「anが等差数列」である場合には次の関係が成り立ちます。
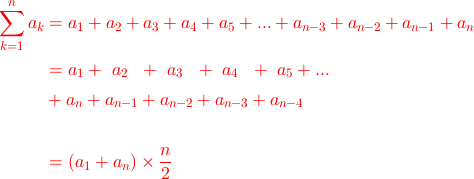
すなわち何度も述べてきた
「 (最初の数+最後の数)×(全体の個数)÷2 」
が成立する、ということです。
これは等差数列を計算する上で非常に重要な計算方法です。
この計算方法を使えば最初に述べていたような

という地道には計算が困難なものでさえも計算できます。
結果は以下のようになります。
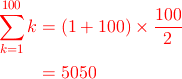
あっという間に計算できましたね!
以下は練習問題になります。
以上が等差数列を簡単に計算する方法になります。
上の練習問題では最後の2つが特徴的な問題ですが、次のページ以降を進めていく上でキーとなる内容を含んでいます。
きちんと数列・シグマΣのイメージを構築した上で先の内容に取り組んでください。
