確率
簡単な問題ではありましたが、同様に確からしいという単語の重要性も分かってきたことかと思います。くれぐれも
同様に確からしいものを数える！ 分母・分子で数える物を変えない！
の2点に注意して以下の問題に取り組んでみて下さい。
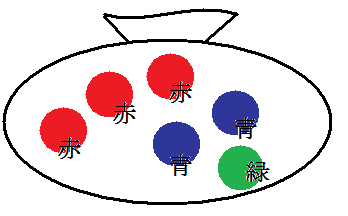
袋の中に赤ボール３つ・青ボール２つ・緑ボール１つが入っています。
この中から無作為に２つのボールを取り出した時に、赤ボール１つ・青ボール１つを取り出す確率を求めなさい。この問題はどうでしょうか？前のページの問題から一気に難しくなった、と感じる方もいるでしょうが、まず確率の問題を解く上で最初にやることはなんでしたっけ？
同様に確からしいものは何か？すなわち分母に何をとるか？でしたね。
まずは自分の答えを出して下さいね。私としてはこの問題での分母の候補として次のような３パターンを選ぶ方がいると思います。
＜Ａさんの場合＞
赤・青・緑と色毎にボールに名前を付けて
右のような赤・青・緑の組み合わせを考えて全部で５通りだ（分母は５）とする。
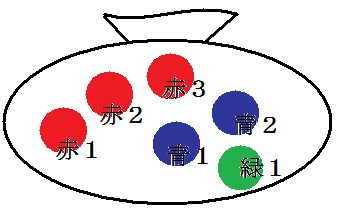
＜Ｂさんの場合＞
赤１?３・青１?２・緑１とボール１つ１つに名前を付けて、6個それぞれを区別して
右のような6種類のボールの組み合わせを考えて全部で１５通りだ（分母は１５）とする。
＜Ｃさんの場合＞
赤１~３・青１~２・緑１とボール１つ１つに名前を付けて、6個それぞれを区別して
ボールを取り出す際に1つ目2つ目と順序付けることで、右のような6種類のボールの順列を考えて全部で３０通りだ（分母は３０）とする。
(順列で考えているので、6種類のボールを区別するだけでなく、取り出す順序も考えている)
さてとりあえずＡ?Ｃの3通りを紹介しましたが、どの考え方は同様に確からしく考えているのでしょうか？
正解はＢとＣの考え方です。Ａさんの考え方だけ間違っています。
Ａさんの考え方は6個のボールを識別していない点が間違いです。そもそもこのような考え方をすると 例えば赤ボールの数が100個や1000個になったとしても分母は変わらず5のままなので、いつでも答えは
です。どう考えても変ですよね？つまり色毎に識別したからといって同様に確からしくはならないのです。
逆にＢさんやＣさんの考え方の場合、きちんとボール6個全て区別しているのでＢ・Ｃどちらも同様に確からしい という結論になります。
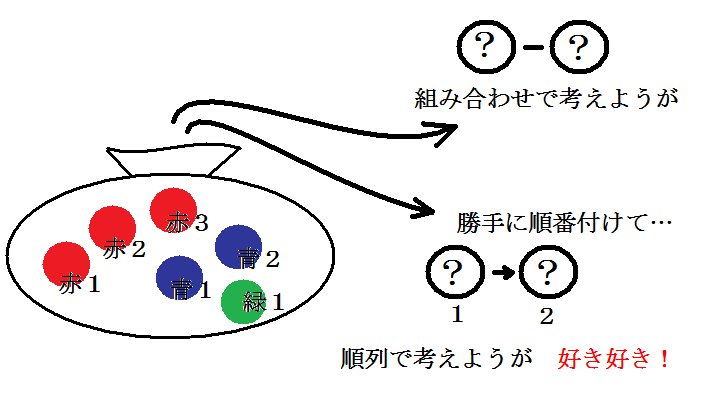
「分母の取り方って一つだけじゃないの？」と思われる方もいると思いますが、1通りとは限りません。前ページのサイコロの問題の場合には解説した1通りぐらいしかありませんでしたが、 問題によって２通りにも３通りにも考えることが可能です。
今回の問題の場合、取りだしたボールの組み合わせを考えようが、勝手に順番をつけて順列と考えて設定しようが、いずれも同様に確からしく考えているのです。
さてこのように分母の取り方が組み合わせで考えるか、順列で考えるか、で２通り出てきましたが答えは１つになるのでしょうか？
ひとつひとつ見ていきましょう。
＜Ｂさんの場合＞
右の１５通りの組み合わせの内、６つが赤と青の組み合わせになっています。よって
と求まりました。図を書かなくても計算で求める方法もあります。
異なるn個の中からｒ個を取り出す組み合わせの総数の書き方コンビネーション
を用いると分母は赤１~３、青１~２、緑１の６つのボールの中から２つを取り出すので
と書け分子は赤１~３の中から１つ、青１~２の中から１つを取り出すので
と書けます。以上の結果から答えは
となり、数え上げた時の結果とも一致します。
＜Ｃさんの場合＞
右の３０通りの組み合わせの内、１２個が赤と青の組み合わせになっています。よって
と求められます。またこちらも図を書かなくても計算で求める方法もあります。
異なるn個の中からｒ個を取り出す順列の総数の書き方パーミュテーション
を用いると分母は赤１~３、青１~２、緑１の６つのボールの中から２つを取り出して並べることで１つ目・２つ目と区別すれば良く
と書け分子は赤１~３の中から１つ、青１~２の中から１つを取り出した後に並べ直すと考えれば良いので
と書けます。以上の結果から答えは
となり、数え上げた時の結果とも一致します。以上の結果をみて分かったと思いますが、順列で考えた場合でも約分をすれば
となり、
組み合わせで考えた場合の結果と完全に答えが一致するのです。よって確率を考える上での最初の手順「同様に確からしいか」という手順で間違えなければ正しい答えに結びつきます。大抵の問題の場合順列まで含めて考えておけば、まず同様に確からしいか、というステップで引っかかる事もないかと思います。
しかし、Ｃさんの解答をみると分かるようにＢさんの解答よりやや煩雑になってしまっています。順列まで考えたために計算量が２倍に増えてしまっているのです。
よって答えとしてはＢさんの解答がよりスマートな解答と言えるでしょう。問題の都度、適切な設定が出来るように気をつけるようにしましょう。
また今回は細かく解説しませんでしたが、
や
といった分母と分子で同様に確からしいとしているものが入れ替わる、
すなわち順列で考えているのか、組み合わせで考えているのか、チグハグになった解答にはしないよう、十分に注意して下さい。