確率
さてでは同様に確からしいものを考えることの重要さが分かった上で、実際の問題の中で活用してみましょう。
実際の問題をとく上では「同様に確からしい」ことに注意するのですが、その中でも間違いが多いのが
分母と分子で数え上げているものが違う
というミスです。これは自分自身も行ってきたミスですし、教えてきた受験生の多くがこのようなミスをしています。
このようなミスをしない上ためには当然何を同様に確からしいとしたか？ということに気を払うのですが、
その中でも特に
順列で数えたか？組み合わせで数えたか？
について気を払うようにして下さい。
前置きが長くなりましたが、以上の事に気をつけて次の問題を見ていきましょう。
大・小2つのサイコロを投げた際に１と２が出る確率を求めなさい。
この問題であれば迷いなく正解出来る方も多いとは思いますが、ここではかなり丁寧に解説します。もし簡単に答えが 出せる、という方は私の経験上この問題で
または
と答える学生がいます。何故そのような答えが
出てしまったのか考えることで、「同様に確からしい」ということへの理解を深めて下さい。確率の問題を解く上でまず最初に行うことはなんだったかというと、クドイようですが同様に確からしいものが何か？でしたね。
確率の問題の答えは知っての通り０?１の間に収まり、通常
のような
分母・分子の構成で答えます。この同様に確からしいものは何か？と考えることは確率の分母が幾つか考えることです。
ですので、この分母を幾つにするかで間違えるとその時点でその問題の不正解が確定します。この操作は非常に注意して行って下さい。では先程の問題ですが、サイコロを２つ振った時の目の組を考えるわけですが、私の経験上、確率の分母として21を選ぶ人と36を選ぶ人とがいます。 それぞれの考え方は次の通りです。
右図をみると分かるように、この人（以下Ａさん）は 1個目・2個目のサイコロに順序付けて
1個目のサイコロに１?６が出る
２個目のサイコロに１?６が出る
という事象を全通り考えています。よって確率の分母は
６×６＝３６
となります。
続いての考え方は右図を全パターンとしている人（以下Ｂさん）です。 この考え方をしている人は1個目・2個目のサイコロで出た目の組み合わせだけを考えています。
よって考え方としては＜１と２の組＞＜３と５の組＞＜３と３の組＞・・・等のように数え上げており、全部で21通りあると分かります。
よって確率の分母としましては
２１
となります。
さて、このように２つの分母の候補が出てきましたが確率の答えはそれぞれ幾つなのでしょうか？
前者Ａさんの方法では
ですし（36個の同様に確からしいものの内、該当するのは２つある）
後者Ｂさんの方法では
となります。（21個の同様に確からしいものの内、該当するのは１つある）
どちらが正しいのでしょうか？
正解は前者Ａさんの解答
だけです。
よって答えは
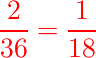となります。後者Ｂさんの解答の何が間違っているのか、というと同様に確からしくないから の一言です。
それ以上の説明が困難なぐらいですが、日常のサイコロを振った経験からいっても分かるかと思いますが、 サイコロというのはサイコロの目６個が同様に確からしく出るように作られた物なのです。
2個のサイコロを同時に振ったからといってそれぞれのサイコロはお互いの結果に依存することなく、１?６の目を好きなように出します。 サイコロ同士が組み合わせを同様に確からしくするように目を出す、というのはありえません。
よってＢさんの解答をもし何かのテストで書けば1行目からバツを付けられます。
以上の説明で分かったと思いますが、６×６＝３６個の組それぞれが同様に確からしいのです。
しかしここまで分かっているのにも関わらず、答えを
と書いてしまう学生を
大変多く見かけます。自分の答えがそうなっていませんか？あるいはどうしてそのような解答を出したのか、分かるでしょうか？
この学生はどう考えたのか、というと分母は先程のＡさんの考え方と同様３６にしたのですが、
分子の数え方だけ組み合わせで考えてしまった
ためにこのような答えになってしまったのです。
自分自身の受験生だった頃もそうだったのですが、学生の答案を見るとこのような答案を非常に多く見かけます。 要するに
分母と分子で同様に確からしいとしているものが違う というミスです。
分母は順列で数えているのに、分子は組み合わせで数えるあるいは
分子は順列で数えているのに、分母は組み合わせで数えるというのがよくあるミスの典型例です。
今回の問題は非常に簡単な問題の例ですが、結局はこういったミスが学生の確率の不出来につながっています。
受験生だった当時、突然確率が分からなくなった、というのもこういったミスを連発するようになったためでした。
同様に確からしい、という単語の重要性が少しは分かってきたでしょうか？
まだ分からない人のためにも、次のページからもう少し難解な問題に触れていきます。