場合の数

 前ページでは実際に１つ１つ数えることで「場合の数」に取り組んでいました。何度も言っていますが、これが最も基礎となる考え方です。 しかし、実践の場においてはこのように１つ１つ数える時間が無かったり面倒であったりするために、掛け算などの計算を用いることで簡単に解くことを行います。

 まずここでは順列について学びます。


１?５の数字が書かれたカードが１枚ずつ袋の中に入っている。袋の中から１枚のカードを取り出し、そのカードの数字を見てから袋の中に戻す。この操作を３回繰り返す時、 出るカードの順列は全部で何通りか？

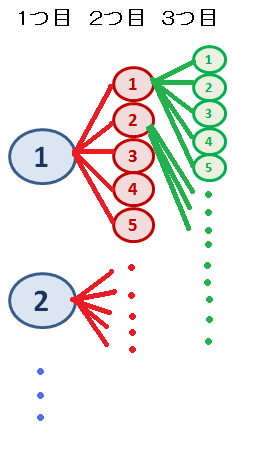　　＜場合の数の画像が表示されていません！＞　　  基本に忠実に解きます。すなわち「１つ１つ数える」ということを一度考えてみます。ここではまず、樹形図を用いて考えることにしましょう。
樹形図とは起こりうる場合の数を調べる時に使われ、ものごとの相違を枝分かれの形で表した図のことです。言葉で言っても伝わらないと思いますので 実際に書くと右図のようになります。

 １回目、２回目、３回目に出るカードの候補を横に並べれば良いのです。例えば「１回目に１が出て、２回目に１が出て、３回目には５が出る」といった具合に全パターンを調べ上げます。
この樹形図を最後まで完成させても良いのですがそれでは少々大変なので、ここで樹形図を参考に考えてみると「１回目には１?５、２回目には１?５、３回目には１?５」という数字が取れると分かります。


 よって答えは　5×5×5 = 53 = 125 すなわち１２５通りが答えだと分かります。
樹形図を用いて考える、というアイディアを大切にして下さい。


１?５の数字が書かれたカードがある。このうち３枚のカードを取り出して並べることで３ケタの数字を作る時、全部で何通りの数字を作れるか？

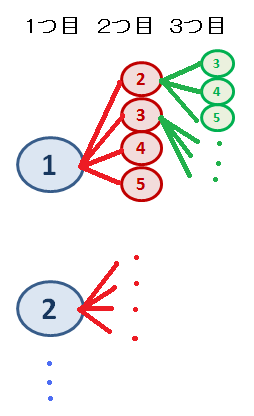　　＜場合の数の画像が表示されていません！＞　　  こちらも樹形図で考えます。先程の問題との違いは「１度引いたカードはもう引けない」という点にあります。そのことに注意して樹形図を作ると右図のようになります。

 例えば１回目に「１」を引くと、２回目以降には「１」を引くことはなくなりますね？なので２回目の引けるカードの候補は２?５になってしまいます。さらに２回目に「２」を引いたとすると ３回目には「２」を引くこともできないので結果３?５のカードのみ引くことが出来ます。このような関係は１回目にどのようなカードを引いたとしても起きるため、１回目に引けるカードの候補１?５の５通りなのに、２回目の候補は４通り、３回目の 候補は３通りとなってしまいます。


 よってこの問題について式をたてると　5×4×3 = 60 すなわち６０通りが答えだと分かります。
樹形図を使うと、式を書いて答えを求めるのに非常に役に立つのです。慣れてくるとこのような問題なら樹形図を書かなくても理解出来ますが、基本的には簡単な問題でも一度樹形図を書いて見ることで大幅にミスを減らす事が出来ます。 是非使いこなすようにして下さい。


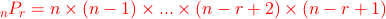
 さらにここで学んでおきたいのが異なるn個の中からｒ個を取り出す順列の総数パーミュテーション 場合の数：数式 です。 まず定義は次のようになります。

場合の数：数式

何やら掛け算がいっぱいならんでいますね。しかし、これだけ見ても一体どんな掛け算なのか良く分からないかと思います。そこでこのように覚えて下さい。
   nPr = [n から１ずつ降りて行ってr個掛け合わせる]
なので例えば 10P3 というと [10 から１ずつ降りて行って3個掛け合わせる]ということで

10P3 = 10 × 9 × 8 = 720

となる、ということです。他にもいくつか例をあげておくと

5P3 = 5 × 4 × 3 = 60
3P2 = 3 × 2 = 6
12P2 = 12 × 11 = 132
12P1 = 12
4P4 = 4 × 3 × 2 × 1 = 24

計算の式自体は簡単に覚えられるかと思います。ここで注意しておきたいのが4P4といった場合です。
このようにPの前後が同じ値である場合には [4 から１ずつ降りて行って4個掛け合わせる] などとなり結局 [4 以下の自然数全てを掛け合わせる]　 ということになります。公式のように書くと

場合の数：数式

と書けます。ここで最後の書き方 n! という記号を見たことが無い方もいると思います。ビックリマークにしか見えませんが、これは「ビックリ」とは読まずに「階乗」と読みます。
4! は 4の階乗 とよび 10! は 10の階乗 とよびます。
この階乗を用いて先程の nPr を書きなおしてみると次のようになります。式変形としては
分母子に (n-r)×(n-r-1)×(n-r-2)×…×3×2×1 を掛けています。

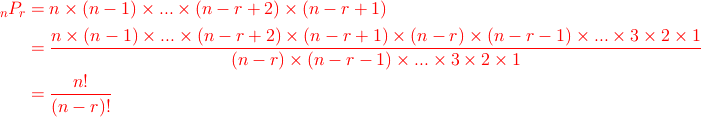
場合の数：数式

このように階乗を用いた書き方をすると非常にスマートな式で書けますね。大学受験などの一部の問題ではこのような表記方法を知らないと問題が扱いにくくなるので、 この書き方も是非覚えて下さい。
簡単な計算をするときなど、感覚的には nPr = [n から１ずつ降りて行ってr個掛け合わせる] という理解が便利です。


　さて、なぜいきなりパーミュテーションの話をしたのかといいますと、このパーミュテーションが順列の問題を解く上で非常に便利だからです。
というのも次のように式を立てられるのです。

　 場合の数：順列　
　　　 異なるn個の中からr個を選んでそれらを並べる順列は全部で　 nPr　通りである。


納得できますでしょうか？これは感覚的には５枚のカードの中から３枚のカードを取り出す話とまったく同じように理解できます。要するに樹形図です。
先程の問題の場合ですとパーミュテーションを使うと 5P3 = 60 通りと求められます。非常に簡単に解けますね。
しかし基本的には樹形図の考え方が一番重要なので、そちらを大事にして下さい。順列の問題だからって全部がパーミュテーションを使えるわけじゃないですよ？毎回一度頭の中だけでも樹形図をイメージすることが大切です。

以下は練習問題になります。

　 場合の数：順列　
　　　 10枚の異なるカードの中から３枚を選んで並べるとき並べ方の総数を求めなさい。

   10P3 = 10・9・8 = 720（通り）


　　　 アルファベット26文字のカードがある。この中の2枚のカードで文字を作るとき、出来る文字列は何種類か？

   26P2 = 26・25 = 650（種類）


　　　 26種類のアルファベットを使って出来る２文字の文字列は何種類か？

   26・26 = 676（種類）
   ※カードの中から選ぶわけではないので２つの文字を重複して使う事が出来る。[kk][cc]など。よって先の問題とは異なる。


　　　 1?7の数字の書かれたカードがある。この中のカードで３ケタの数を作るとき何通りの方法があるか？

   7P3 = 7・6・5 = 210（通り）


　　　 1?5の数字の書かれたカードがある。この中のカードで５ケタの数を作るとき何通りの方法があるか？

   5P5 = 5! = 5・4・3・2・1 = 120（通り）


　　　 0?6の数字の書かれたカードがある。この中のカードで３ケタの数を作るとき何通りの方法があるか？

   百の位,十の位,一の位の順番で数を決める。

   百の位・・・0にすることは出来ないので 1?5 のいずれかの数にする。つまり５通り。
   十の位・・・百の位で選んだ数以外であればなんでも良い。十の位は0でも良いので５通り。
   一の位・・・百の位,十の位で選んだ数以外であればなんでも良い。一の位も0でも良いので４通り。

   以上を踏まえると
   5・5・4 = 100（通り）
   ※0があるときは要注意！0を一番高い位の桁に置くことはできません。


パーミュテーションの使い方が分かったでしょうか？使えるときは簡単に式をかけますが、使えない場面も結構あるのです。その都度、頭で樹形図をイメージすることが大切です。 丁寧に問題に取り組みましょう。