面積を求める

難解な面積

 ある領域の面積を求めたいという欲求は、あらゆる場合で起こります。 それが長方形や円の面積であれば、それらの求め方は高校生ならすでに知っていると思います。 しかし、これがもし以下の図に示すような領域だったらどうでしょう？
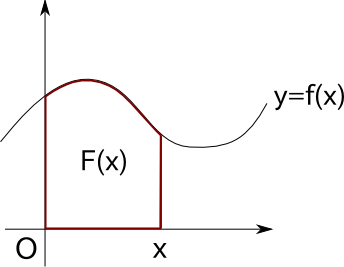
fig5-1.png
こんな面積とても求められる気がしませんよね？

 しかし諦めてはいけません。少し考えてみましょう。 まず、図のような面積を表す関数をF(x)とします。 次に、xの値を微小量Δxだけ大きくしてみます。
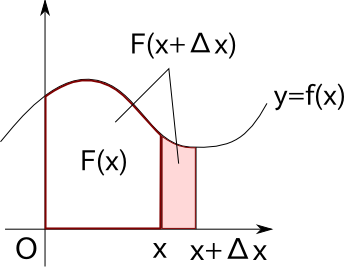
fig5-2.png
このとき、図のピンク色で示した部分の面積を考えてみます。 もちろん正確には分かりません。しかし、Δxが非常に小さい値であるとすると、 長方形で大体の面積を近似できるはずです。 具体的には、横がΔx、縦がf(x)となる長方形と大体同じ面積になります。
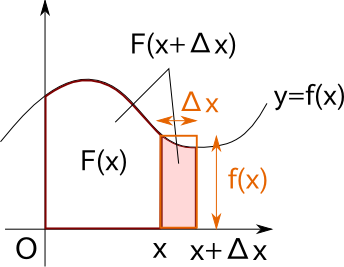
fig5-3.png
 また、この面積というのはF(x+Δx) - F(x)と表すことができます。 すると以下の式が成立します。
fm5-1
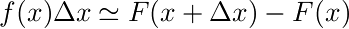
この式を少し変形してみましょう。
fm5-2

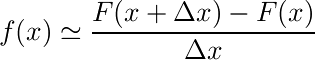
 どうでしょう。なんだか見覚えのある形になってきたと思いませんか？ そう、これは微分の定義式によく似ています。ここでΔx→0とすれば、 これは完全に微分の定義式そのものです。
fm5-3
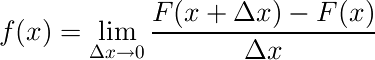
 さらにこの式の両辺を積分してみましょう。
fm5-4
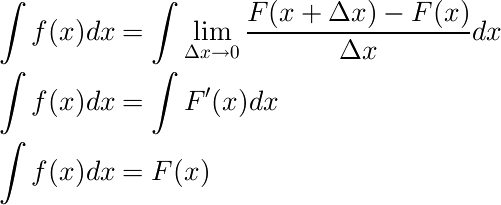
 この式は驚くべきことを表しています。なんと関数f(x)を 積分すると、最初の図に示した部分の面積を表すことになるのです。 これはすごい！

積分には2種類ある

 さて、上で示したように、積分には面積を求めるという非常に重大な役割があります。 つまり、積分には2種類あることになります。

  • 微分の逆演算としての積分
  • 面積を求めるための積分
このような分類をすると、数学のプロの方に怒られるかもしれません（笑） しかし気分としては大体この二つに大別できると思います。そして一つ目の積分を不定積分、 二つ目を定積分と呼びます。

 ここまでの内容ではまだ定積分の説明が不十分なので、次回もう少し話を続けることにします。