積分は本当に微分の逆演算か?
奇妙な問題
ちょっと奇妙な話をしましょう。今、f(x) = x + 3であるとします。まずはこの関数を微分してみましょう。
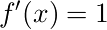
では次にf'(x)を積分してみることにします。するとおかしなことに気付くはずです。
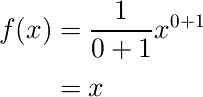
そうです。もとの式にあった+3が消えてしまいました。積分が微分の逆演算ならば、微分して積分すれば
もとに戻るはずです。一体どうしてこんなことになったのでしょう?
微分が抱える重大な欠陥?縮退
ここでもう一度微分するときのことをよく思い出して下さい。微分するときって、定数項はどうしていましたか? 定数の微分は0ですよね。つまりf(x)の中の+3の部分は微分により消えてしまいます。しかしそうなると、 もしf(x) = x + 4であったとしても、微分すれば同じ式になってしまいます。もっと一般にf(x) = x + C (Cは定数)の微分は、Cの値によらず同じになります。
そうなると、前のページで述べた積分公式を変更する必要がありそうです。冒頭の例でいえば、 f'(x) = 1であれば、f(x) = x + 3としなければいけません。このように、積分をするとかならず 最後に定数項が現れます。
え、ちょっと待って下さい。そもそも積分したいときというのは、積分した結果がどうなるか分からないから 積分がしたいんですよね?今みたいに最初から「f(x) = x + 3 だ」と分かっているならそもそも積分計算 などする必要がありません。つまり、実際の問題ではf'(x)のみが与えられ、そこからf(x)を計算することになります。 しかしそうなると、積分結果に加える定数の値が分かりません。なぜならf(x) = x + 3でもf(x) = x + 100でも、 f'(x) = 1となり、結果は同じだからです。f'(x) = 1とだけ言われても、f(x) = x + 3が正解なのかf(x) = x + 100が 正解なのか判断できません。どっちが正しいのかを判断するための情報がないのです。
以上の議論により、微分の持つ重大な性質が浮かびあがります。それは微分をすると情報が減ってしまうということです。 微分の持つこのような性質のことを縮退といいます。
結果として、減ってしまった情報の分、定数項の値が決められないので、積分を行ってもとの関数を完全に再現するのは 不可能となります。 そこで、実際の積分計算では、f'(x) = 1であれば、これを積分したものはf(x) = x + Cということにします。 このCのことを積分定数といい、微分のせいで失われた情報の補填をしています。「Cの正確な値は分からないが、 とにかく定数項が存在するのは間違いないから、とりあえずCとでもしておこう」ということです。
長くなりましたが、正確な積分の公式は以下のようになります。
