増減表の書き方
導関数の正負
前のページでの疑問をここで解消しましょう。導関数が0になる点が極大点なのか、極小点なのか、 そのどちらでもないのかを見分けるには、増減表というものを書きます。しかしその前に もう一つ簡単な事実を確認しておく必要があります。それは導関数の値の正負と接線の傾きの関係です。 これはもう半ば明白で、導関数の値はその点での接線の傾きに一致するわけですから、 導関数の値が負になるような点では接線の傾きは負になり、逆に導関数の値が正になるような点では 接線の傾きは正になります。
ここでもう少し突っ込んでみます。接線の傾きが負であるような領域というのは、実は
関数がどんどん減少していく領域になっており、逆に接線の傾きが正であるような領域では
関数はどんどん増加していきます。例えば放物線の左半分と右半分を思い浮かべれば、これは
当たり前のことだと言えます。
面倒だが書くしかないのだ
以上を踏まえた上で増減表の話に戻ります。増減表とは、x、f(x)、f'(x)の関係を表にまとめたものです。 具体的な書き方の手順は以下のようになります。
ここでは例としてf(x)=x3 + 3x2-9x + 1の増減表を
書いてみましょう。
まずf(x)をxで微分します。
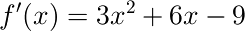
次にf'(x)=0となるxを求めます。f'(x)=0ということは、つまり傾きが0になるxを求めるわけですね。
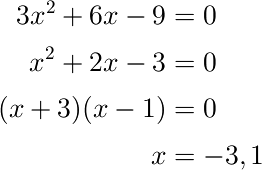
上で得られたx=-3,1を表に書き入れます。また、当然この時のf'(x)の値は0となるので、それも書き入れます。
| x | ・・・ | -3 | ・・・ | 1 | ・・・ |
|---|---|---|---|---|---|
| f'(x) | 0 | 0 | |||
| f(x) |
そして、上で得られたx=-3と1の間、および外側から適当な値を選びます。これは何でもよいのですが、ここでは -4, 0, 2を選ぶことにします。これをf'(x)に代入します。
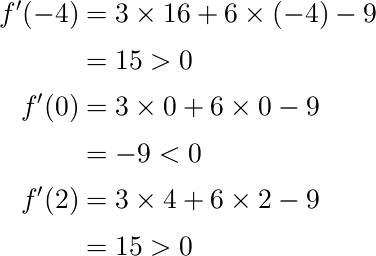
これよりx=4でf'(x)>0、x=0でf'(x)<0、そしてx=2でf'(x)>0と分かりました。これに従ってf'(x)の欄に+、および-を記入します。 さらにそれをもとに、f(x)の欄に右上矢印、右下矢印を書き込みます。
| x | ・・・ | -3 | ・・・ | 1 | ・・・ |
|---|---|---|---|---|---|
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | ↘ | ↗ |
表を見ると、x=-3の左側では値が増えており、逆に右側では減っていることが分かります。これはつまり、 x=-3でピークを取ることを意味します。つまりx=-3では極大になることが分かります。また、x=1の左側では値が 減っており、右側では増えていきます。これより、x=1では極小になるということが分かります。最後にこのときの f(x)の値を求めて、表に書き込みます。
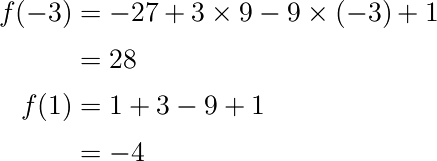
| x | ・・・ | -3 | ・・・ | 1 | ・・・ |
|---|---|---|---|---|---|
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 28 | ↘ | -4 | ↗ |
以上より、極大点は(x,y)=(-3,28)、極小点は(x,y)=(1,-4)であることが分かりました。
