微分って何？

2種類の速さ

 中学の理科で「平均の速さ」というものを習ったのを覚えているでしょうか？ 例えば車の例でこれを考えてみます。 車というのは最初は止まっていて、アクセルを踏むと加速し、ある程度加速すると 一定の速度で走るようになり、信号などでブレーキを踏むと減速します。 このように考えると、車の走る速さというのは常に一定ではなく、 時々刻々と変化しています。しかし中学の理科では、 途中でいろいろと速さは変化しつつも、最終的に（例えば）1時間に40km進んだのなら、 速さを40km/hとしていました。これが平均の速さです。
 しかしこの値に意味はあるのでしょうか？まったくないとは言いませんが、 途中で止まったり猛スピードで走ったりを断続的に繰り返しているにも関わらず、 それを単に40km/hとしてしまうのはいささか強引な気がします。 そこで「瞬間の速さ」の登場です。瞬間の速さとは文字通りその瞬間にどれだけの 速さで走っているのかを表すものです。車の速度計が示しているのがまさにこの瞬間の速度ということになります。
 しかし、瞬間の速さなんて一体どうすれば求まるのでしょうか？この疑問に答えるのが今回の主役である微分というわけです。

 またまた車の例で考えてみましょう。今、車がスタートから3秒後に30m地点を走っているとします。 そこから加速して、(スタートから)5秒後に60m地点に到達したとします。 このときの平均の速さを求めると、(60-30)/(5-3)=15m/sとなります。
 スタートから5秒後には60m地点にいたわけですが、では4秒後に40m地点に居たとしたらどうでしょう？ この場合の平均の速さは(40-30)/(4-3)=10m/sとなります。同様に、3.5秒後、3.1秒後、3.01秒後、3.001秒後というように どんどん3に近い時刻との間で平均の速さを計算するとどうなるでしょう？ 実は、このように3秒後と3に限りなく近い時刻との間の平均の速さを求めると、3秒後の 瞬間の速さに限りなく近づいていきます。 このように考えると、瞬間の速さとは超微小時間の間にどれだけの距離移動するかを 表したものであるということができます。

これを少し数式を使って一般化してみます。ある時刻tからt+Δtまでの間に、xの値がx+Δx に変化したとき、この間の平均の速さは

fm1
と書けます。ここで、Δtを限りなく小さくしていくと、同時にΔxも小さくなっていき、 時刻tにおける瞬間の速さにどんどん近づいていくことになります。このように、ある変数がある値に 近づいていくことを極限といいます。

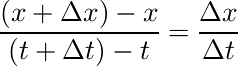
結局微分とはなんなのか？

 以上のことを図に書いてみましょう。
fig1
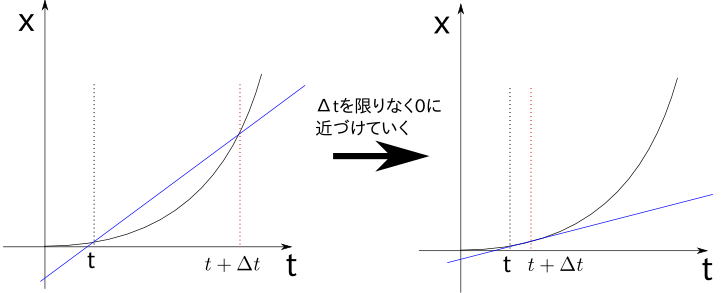
図を見ると、平均の速さというのはある二つの時刻を直線で結んだときの、 その直線の傾きを表していることが分かります。では、この二つの時刻というのを限りなく近づけてみたらどうなる でしょうか？これはなんとグラフの接線の傾きを表すことになるのです。実は瞬間の速さを求めるということは、 数学的にはグラフの接線を求めることに相当しているのです。

 今まではなんだか物理の話でしたが、グラフの接線を求められるというのなら数学でも大いに役立つはずです。 上で議論した内容を数学的に書き下してみましょう。
 ある関数f(x)について、xの値がΔxだけ増加するとき、 f(x)の値はf(x)からf(x+Δx)に変化します。このとき、xにおける f(x)の接線の傾きは、上の議論より

fm2
となります。limは極限を表す記号で、ここではΔxが限りなく0に近づくということ>を意味します。 このようにして得られた新たな関数f'(x)のことをf(x)の導関数と呼びます。 そして、この導関数を求めるための操作のことを微分と呼ぶのです。

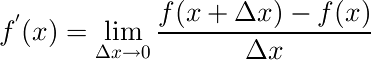
以上をまとめると以下のようになります。

　 微分　
関数f(x)について
fm2
のようにして得られる関数f'(x)を、f(x)の導関数と呼び、f'(x)を 求めることをf(x)を微分するという。実用的には、 微分とはf(x)のxにおける接線の傾きを求める操作である。

 導関数についてもう少し説明します。 f(x)を微分することで得られる導関数f'(x)は、これまたxの関数です。 これはつまりどういうことになるのかというと、f'(x)のxに好きな値を代入すれば、その点での f(x)の傾きが求まるということです。例えば、x=3でのf(x)の傾きはf'(3)になる、ということです。 導関数さえ求めれば、このようにしてあらゆるxに対して接線の傾きを求めることができます。