三角関数

　上の問題全てが時間をかけずに頭の中で解答を作れる人は以下は読み飛ばして問題ないです。 しかし初めて見た人、あるいは暗記している人絶対に読んで下さい。
　特に暗記している受験生がビックリするほど多いので、逆に感心します。こんな公式覚えるモンじゃないです。 っというか覚えられません。何人かの東大生に聞いてみましたが、この公式を 覚えている学生は一人もいませんでした。皆頭の中で考えて解答してきたようです。

　そこで頭の中でどうやってすぐさま答えを叩き出すのか、その手順を追ってみました。
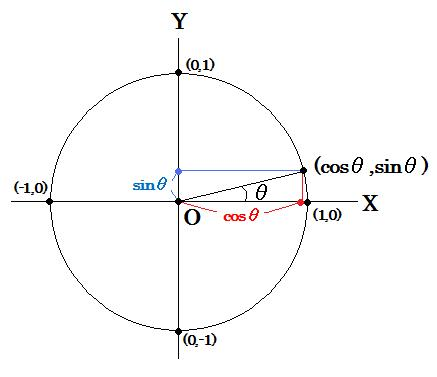
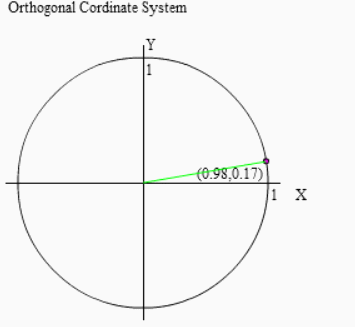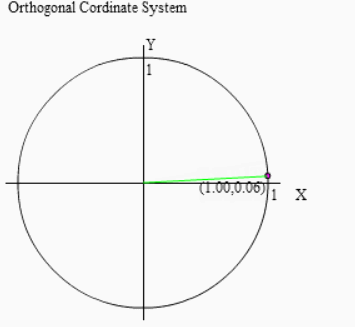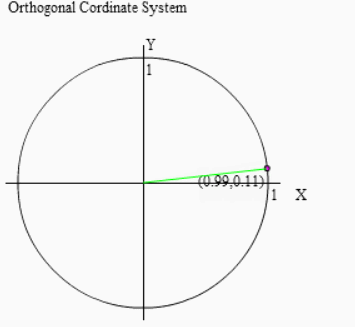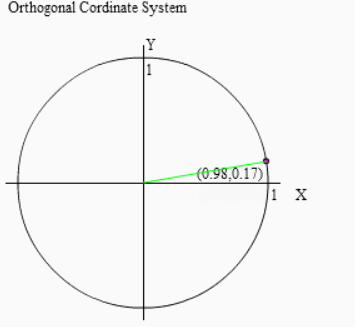
　まず右図のように小さな角θ（20°以下位がベスト）によってcosθ,sinθを用意して下さい。θ回転したときのX座標がcosθ、Y座標がsinθだったので、右上図のようになりますね。ここで注意しておきたいのが、cosθ > sinθ ということ。平たく言えば
大きい方がcosθ、小さい方がsinθとなっていることを忘れないで下さい。

---

では今作ったθを使って (180°-θ)回転したときの点とは一体どこの点か おおよそでいいので場所は分かりますか？？

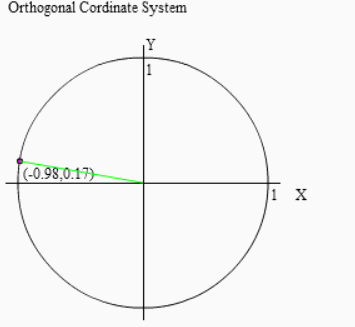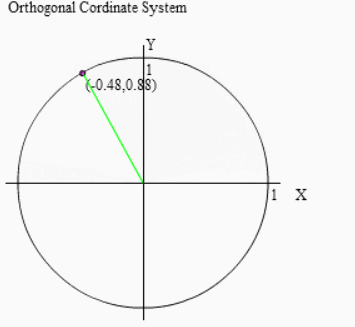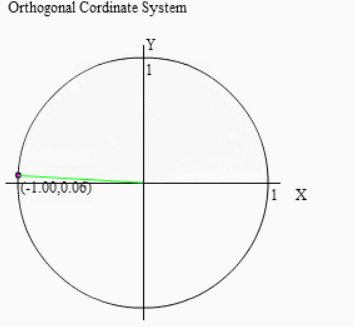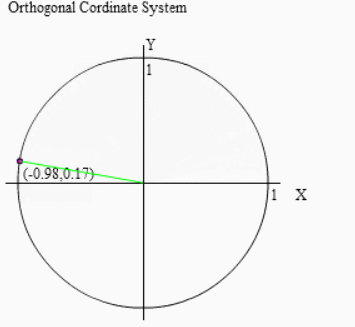
(180°-θ)回転とは「180°回転したあと、(-θ)回転する」ということですから、右図のように先ずは180°回転させましょう。
その後　θ　だけ逆回転することで (180°-θ)回転を実現します。よって行いたい操作全体としては右図のように行えば良いのです。

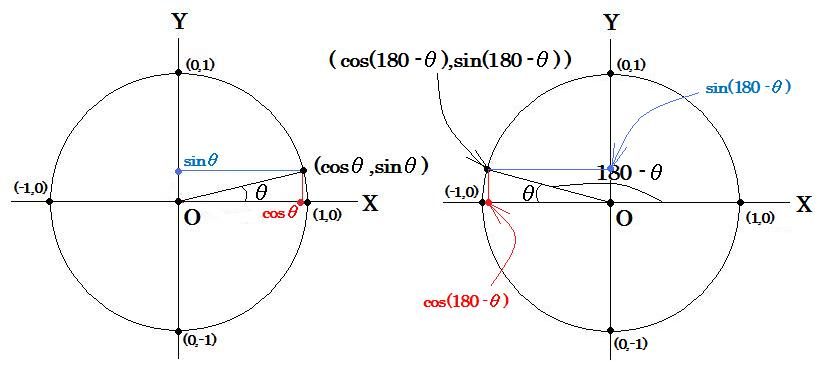
　上の２つのグラフの内の右が正解の図になります。
　ではcos(180-θ),sin(180-θ)とは一体どこのことを言うのかというと、元の定義に沿って書けば
原点から出た(1,0)方向の矢印が、原点周りに(180-θ)回転した時のX座標をcos(180-θ)、Y座標をsin(180-θ)
　となります。よって上図に示したX座標、Y座標がそれぞれcos(180-θ)、sin(180-θ)という値になる、ということです。
　ここまで付いて来れていますでしょうか？
　付いて来れた人は『この座標の大きさ・・・これって何かと同じじゃない？？』と感じませんか？

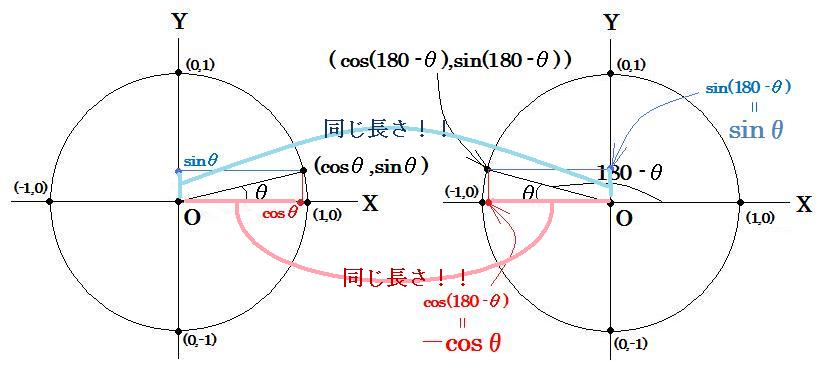
　上図を見ると分かるように実は元の図形上のcosθ,sinθと同じなのです。
　ただしcos(180-θ)は負の値であることに注意すれば

cos(180-θ) = -cosθ
sin(180-θ) = sinθ

となります。これがさっきの問題の１つ目の解です。

---

　では次に　cos(90-θ),sin(90-θ)　についても考えてみます。
　(90-θ)回転した点とはどこか　図に示せますか？これが慣れてきて頭の中で描ければ東大頭脳です。

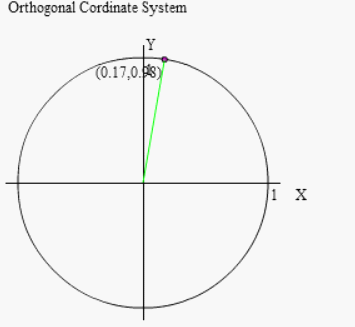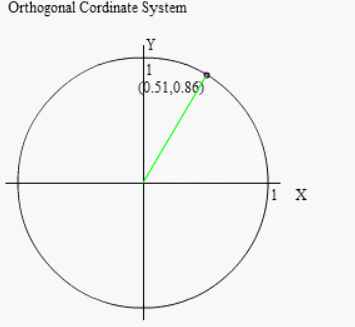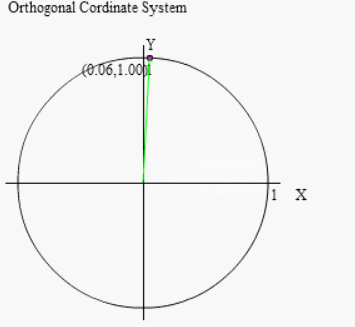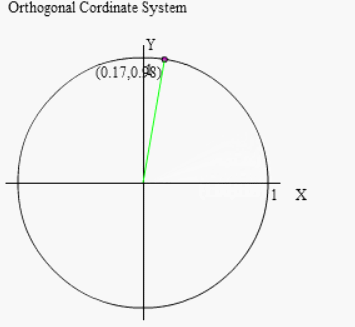
先程と同じように行いましょう。
(90°-θ)回転とは「90°回転したあと、(-θ)回転する」ということですから、右図のように先ずは90°回転させましょう。
その後　θ　だけ逆回転することで (90°-θ)回転を実現します。よって行いたい操作全体としては右図のように行えば良いのです。

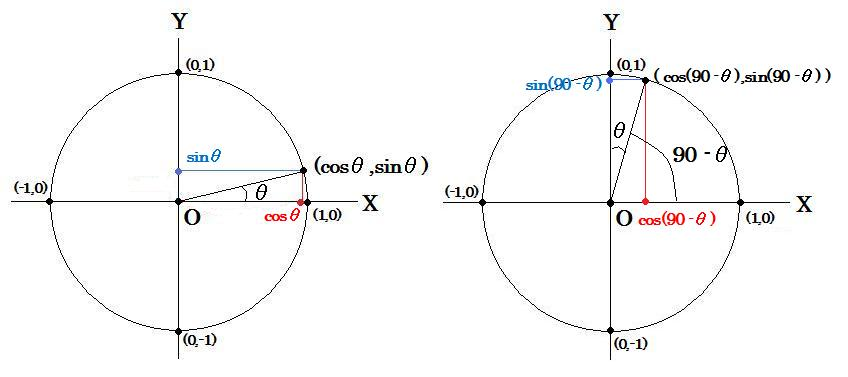
　これが正解の図です。
　さて、ではcos(90-θ)、sin(90-θ)とは一体なんでしたっけ？ そしてその大きさは何かと同じじゃないでしょうか？？

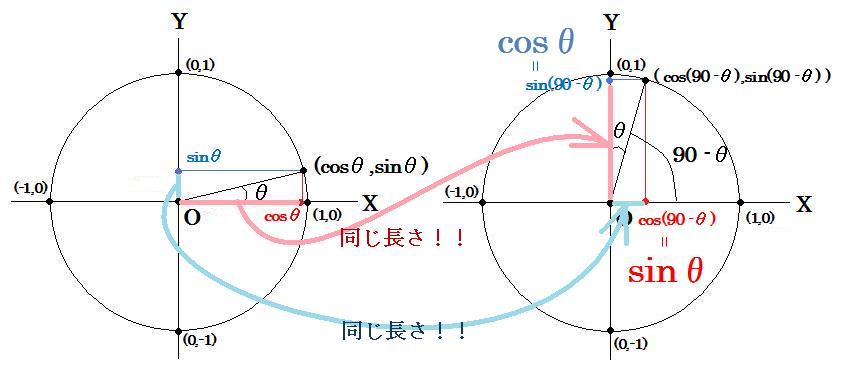
　原点から出た(1,0)方向の矢印が、原点周りに(90-θ)回転した時のX座標をcos(90-θ)、Y座標をsin(90-θ)
　よって上図を見ると分かるようにcos(90-θ)、sin(90-θ)は実はそれぞれ元の図形上のsinθ,cosθと同じなのです。
　ちょうどsin,cosが逆転した様子になりますね。

cos(90-θ) = sinθ
sin(90-θ) = cosθ

　となります。これがさっきの問題の２つ目の解です。結局この手の問題の解は「cosかsinにマイナスがついた程度」だけです。
　つまり
　　　　回転したときのX座標・Y座標はcosθ、sinθどちらの長さに等しいですか？ という話になります。
　最初にθは小さく取ったので大きい方がcosθ、小さい方がsinθとなっていることに注意すれば すぐさまcosθかsinθの判別は出来ますね？
　こんな処理が出来るようになればすぐにこの手の問題の解を求められるのです。

---

　では念のためもう一つ　cos(90+θ),sin(90+θ)　についても考えてみます。
　まず何をしましたっけ？そしてどう求めるか、ストーリーが出来ていますか？？

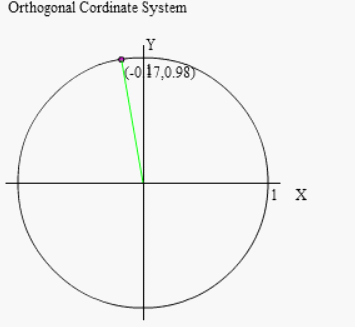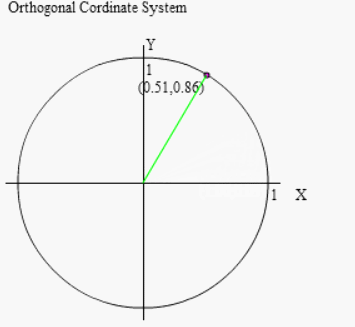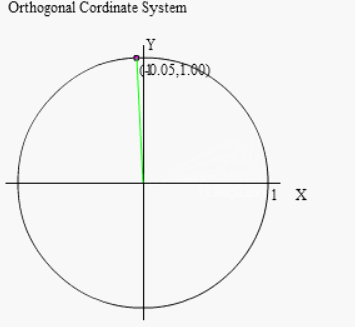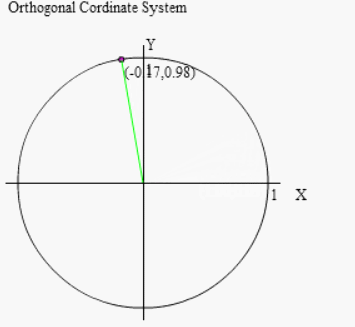
まずは回転した点はどこか？でしたね
(90°+θ)回転とは「90°回転したあと、(+θ)回転する」ということですから、右図のように先ずは 90°回転させましょう。
その後　θ　さらに回転することで (90°+θ)回転を実現します。よって行いたい操作全体としては右図のように行えば良いのです。

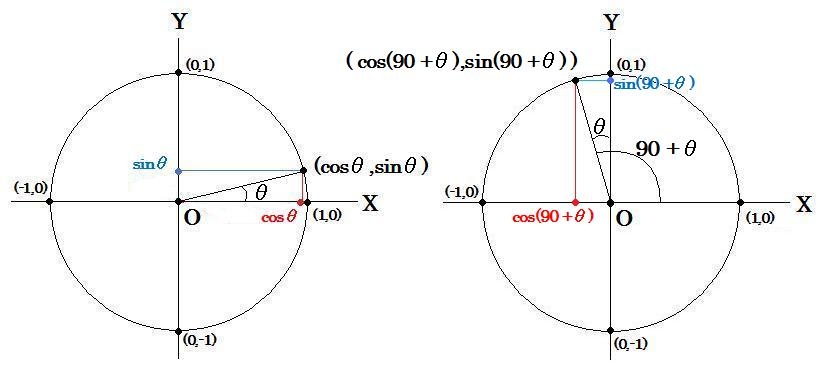
　よってこれが正解の図です。そしてcos(90+θ)、sin(90+θ)を求めるには何を考えるかというと・・・

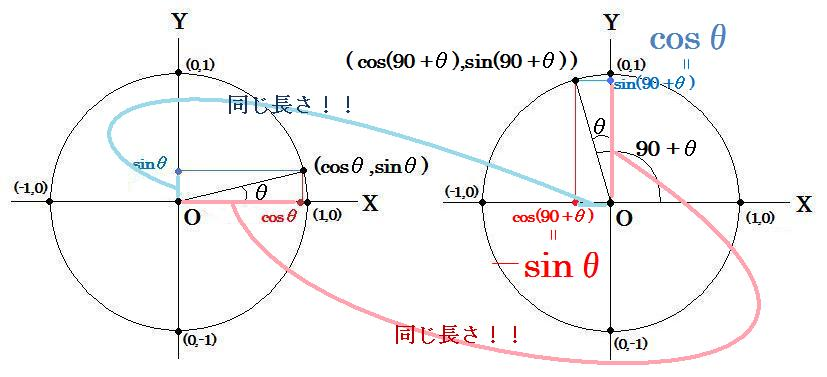
原点から出た(1,0)方向の矢印が、原点周りに(90+θ)回転した時のX座標をcos(90+θ)、Y座標をsin(90+θ)
　よって
cos(90+θ) = -sinθ
sin(90+θ) = cosθ

となります。これがさっきの問題の３つ目の解です。ご理解頂けたでしょうか？

---

さて、今一度下の問題を見てみましょう。最初に見た時よりも、簡単な問題に見えるはずです。
慣れると圧倒的に速く正確に解ける解法ですので、残りの問題は自分で試してみましょう。

問.　次の式をθを用いたより簡単な式に直しなさい 　(1_1)　cos(180-θ)　　　 (1_2) sin(180-θ) 　(2_1)　cos(90-θ) 　　　 (2_2) sin(90-θ) 　(3_1)　cos(90+θ) 　　　　(3_2) sin(90+θ) 　(4_1)　cos(180+θ) 　　　(4_2) sin(180+θ) 　(5_1)　cos(270-θ) 　　　(5_2) sin(270-θ) 　(6_1)　cos(360-θ) 　　　(6_2) sin(360-θ)

解答はこちら