三角関数

　今までは三角形でcos,sinを考えてきたのですが、最初にも述べたようにこのような定義の仕方では角度が180°を超えたときの定義がしづらいですし、 そもそもcos,sinの本質に触れているとは言えません。

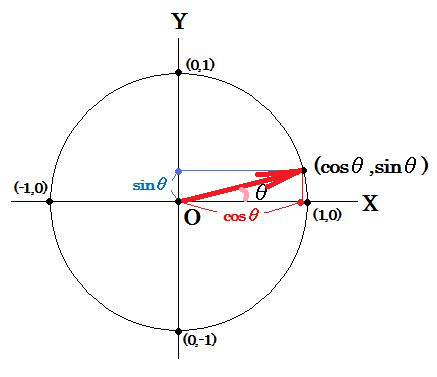
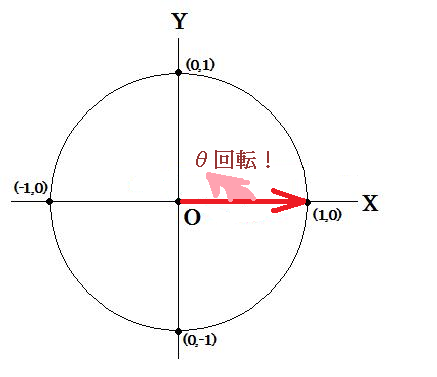
　そこで次のように考えます。まず左上図のような半径が１で原点を中心とする円（単位円と呼ばれている）を用意します。
まだ円の式( X² + Y² = 1 )を見たことはない人もいるかと思われますが、気にしないで下さい。単なる円がそこにある、とだけ思ってくれればいいです。
　この時cos,sinの定義とは

原点から出た(1,0)方向の矢印が、原点周りにθ回転した時のX座標をcosθ、Y座標をsinθ

となります。少々長いですが、ビジュアル化してみると要は上図の通りです。まずは左上図の赤色の矢印を用意して下さい。それを反時計回りにθ回転させ右上図のような矢印を作って下さい。このとき得られた点のX座標をcosθ、Y座標をsinθとして定義している、ということです。回転の方向は数学ではこのように反時計回りに見ることが多いので注意して下さい。
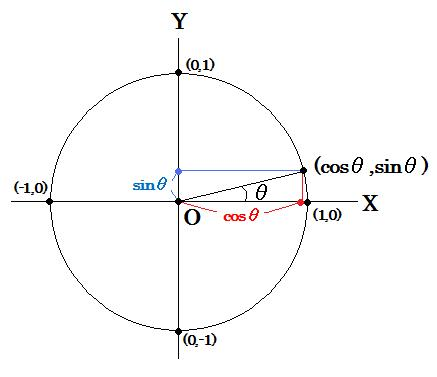　視覚的にどれがcosθでどれがsinθか分かりましたでしょうか？？



平たく言えば
右図の円上の点におけるX座標がcosθ、Y座標がsinθです。
　これならθが180度を超えても問題なく定義できますね。

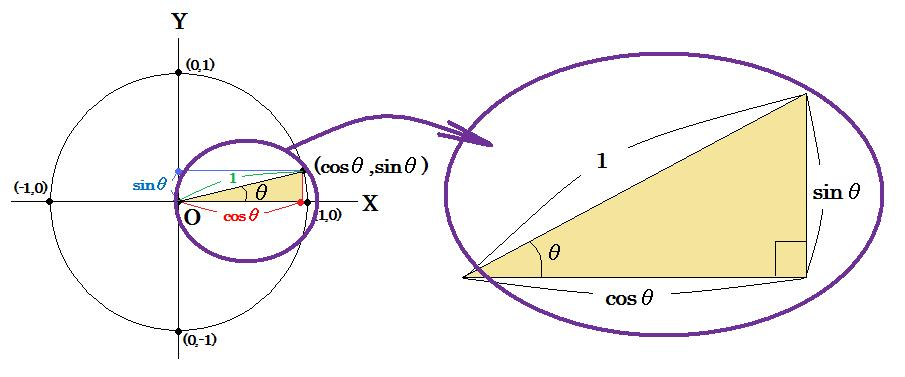
　さて今回cos,sinの定義を新しく書いて見たわけですが、実は以前に書いた直角三角形の定義したcos,sinとまったく同じものを表しています。
　 なぜでしょうか？上の図をご覧下さい。
　右側の図は以前に三角形で解いた時の解答そのものでしたね。三角形の話というのは上図で丸でくくった部分の話だったのですね。

　上図はcos,sinを求めるサンプルです。マウスを動かすとそれに応じて点が動きます。点の横にその時の(X,Y)座標が表示されるので、 それぞれがその角度での(cos,sin)の値に対応します。
(21.3.19追記)Adobe Flash Playerの停止に伴い、図を変えました。円周上を点が動いたときの、(X,Y)座標を表示しています。