２次方程式

　　　?Break Time?

 さて、今まで因数分解・平方完成・解の公式という分野について学び、2次方程式を解くということを目的に説明してきました。
いうなれば2次方程式を解くために因数分解等を学んできたわけですね。
しかしここで手段と目的をひっくり返して
因数分解をするために2次方程式を解くということを行います。

---

　 x²+2x-1 を因数分解しなさい。

 今までのページでも扱った数式ですが、今までの知識でこの式を因数分解しようとしてみても、２つの数を掛けて「-1」、足して「+2」になるような 有理数というのは見つかりません。
しかし、知っての通り x²+2x-1 = 0 を解く、ということは行ってきたわけです。この解を解の公式によって求めることで因数分解を行います。


 何を言っているのか分からないと思うので、以下で詳しく解説します。
x²+2x-1 = 0 の２つの解をα・βという２つの記号でおいてしまいます。
一見記号で分かりにくいと感じる人もいるでしょうが、α・βとはただの数です。
さらに具体的にいえば、実際に解の公式を用いると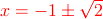と求められるので
   α = 1 + √2
   β = 1 - √2  (α = 1 - √2,β = 1 + √2 でもいいです)
ということです。α・βが x²+2x-1 = 0 の２つの解だというのは頭に入りましたか？？

 さてここで確認したいのですが、 x²+2x-1 = 0 にx = α,βを代入すると式が成立する、ということです。
そのようなxを求めようとしていたので当たり前ですよね？なので例えば
    α²+2α-1 = 0
    β²+2β-1 = 0
という式が成立する、というわけです。ここまで当たり前に見えていますか？

 ところでxの2次方程式でx = α,βを代入すると0になるという式が成立するものの例を１つ挙げてみて下さい。
そのような式といったら・・・
ずばり(x - α)(x - β) = 0がそうですよね？
何が言いたいかというと・・・
x²+2x-1 はx = α,βを代入すると0
(x - α)(x - β) はx = α,βを代入すると0

 要するに x²+2x-1 = (x - α)(x - β)となるんです！（※　若干議論は曖昧ですが直観的に正しいと感じてくれれば良いです）

 今までの長い話を要約しますと
x²+2x-1 = 0 の２つの解をα・βという２つの記号で表すと
x²+2x-1 = (x - α)(x - β)と式変形できる
ということです。(だって左辺も右辺もx=α,βを代入して0だもん！)

 では、今回の問題 x²+2x-1 の因数分解ですが
   α = 1 + √2
   β = 1 - √2
なので
x²+2x-1 = (x - α)(x - β)
    = {x - (1 + √2)}{x - (1 - √2)}
    = (x - 1 - √2)(x - 1 + √2)
と因数分解できます。

このように解の公式を使って2次方程式の解を求めることでどんな2次式でも因数分解できるのです。
では次の例題も取り組んでみましょう。

---

　 2x²-9x-1 を因数分解しなさい。

 今回は x² の係数が今回は 1 でないので若干の注意が必要です。
因数分解したときに 2x²-9x-1 = (x - α)(x - β) とは成り得ませんよね。
今回は x² の係数の帳尻を合わせるために 2x²-9x-1 = 2(x - α)(x - β) となる必要があります。


つまり
2x²-9x-1 = 0 の２つの解をα・βという２つの記号で表すと
2x²-9x-1 = 2(x - α)(x - β)と式変形できる
ということです。(だって左辺も右辺もx=α,βを代入して0だもん！)

また 2x²-9x-1 = 0 の２つの解は
    ∴x = 9/4 ± √89 / 4
となることに注意すると
2x²-9x-1 = 2(x - α)(x - β)
    = 2{x - (9/4 + √89 / 4)}{x - (9/4 - √89 / 4)}
    = 2(x - 9/4 - √89 / 4)(x - 9/4 + √89 / 4)
となります。こちらも通常では解く事の出来ない因数分解を解の公式を用いることで簡単に求めることができました。
以上の手順を一般化してまとめると次のようになります。

　 解の公式を用いた因数分解・まとめ　

　　　 ax²+bx+c の因数分解をしなさい

   ax²+bx+c = 0 の２つの解をα・βという２つの記号で表すと
   ax²+bx+c = a(x - α)(x - β)と因数分解できる
  ということです。(だって左辺も右辺もx=α,βを代入して0だもん！)

  ただし ax²+bx+c = 0 の２つの解α・βは
   　　とする

さてあとはいつものごとく練習です。解の公式を用いることで次の因数分解を行ってみて下さい。

　 解の公式を用いた因数分解：例題　

　　　 x²-10x+3 の因数分解をしなさい。

　 x²-10x+3 = 0　の解を求めると
　∴　x = 5 ± √22
　よって　 x²-10x+3 = {x - (5 + √22)}{x - (5 - √22)}

---

　　　 x²+5x+3 の因数分解をしなさい。

　 x²+5x+3 = 0　の解を求めると
　∴　x = - 5/2 ± √13 / 2
　よって　 x²+5x+3 = {x - (- 5/2 + √13 / 2)}{x - (- 5/2 - √13 / 2)}

---

　　　 4x²+8x+1 の因数分解をしなさい。

　 4x²+8x+1 = 0　の解を求めると
　∴　x = - 1 ± √3 / 2
　よって　 4x²+8x+1 = {x - (- 1 + √3 / 2)}{x - (- 1 - √3 / 22)}

---

　　　 7x²+9x+2 の因数分解をしなさい。

　 7x²+9x+2　の解を求めると
　∴　x = - 9/14 ± 5/14  (すなわち、x = - 1 , - 2/7)
　よって　7x²+9x+2 = {x - (- 1)}{x - (- 2/7)}
　      = (x + 1)(x + 2/7)

---

　　　 x²-18x+81 の因数分解をしなさい。

　 x²-18x+81 = 0　の解を求めると
　∴　x = 9   　「√」　の中が "0" なので答えは一つだけになる。
　よって　 x²-18x+81 = (x - 9)(x - 9)
　      = (x - 9)²

 以上になります。実は全ての問題が前ページの問題から持ってきています。
重要なのは何か？というと解の公式を使って2次方程式の解を求めることでどんな2次式でも因数分解できるということです。
この単元は頑張れば中学3年生にも理解出来る単元ではありますが、センター試験でも取り上げられるほど重要な内容だったりします。さらに重要なのが、次のページから説明する解と係数の関係の 理解において非常に重要な内容です。きちんと理解しておくようにしましょう。