２次方程式
前ページでは
(x + 2)(x + 20) = x2+22x+40 ・・・（※）
といった計算が暗算でも出来るように、という話をしてきました。
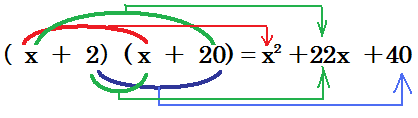
先程のページでなんで展開の説明をしたの？と思われる方もいるでしょうが、因数分解とは実は展開の逆の操作をすればいいだけなのです。
つまり上の（※）式において右辺から左辺を作れれば良い、という話です。ではどうすれば右辺から左辺が作れるか、考えてみて下さい。
しばらくの間は簡単のため x2の係数が1のものだけ、すなわち x2+bx+c の形のものだけを扱います。
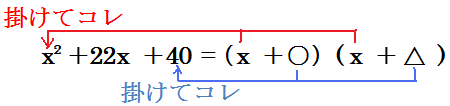今ここで x2+22x+40 の式を因数分解することを考えます。展開の時にも感じたことと思いますが、 x2の項 と 定数項 は簡単に求められる、という特徴がありました。その特徴を今回も利用します。
さらに今 x2の係数が1のものを考えているので、答えは必ず(x + …)(x + …)の形になります。
x2の項 と 定数項 については展開の際に掛け算をするだけで求められる、という話でしたので、今 x2の係数が1であることを踏まえると 1×1=1 としないと x2 の係数を1にすることは出来ませんよね？
よって x2の係数が1ならば(x + …)(x + …) と表記出来るということになるのです。
(x + …)(x + …)という形が答えだと分かってしまったので、右図のように解答用紙にさっそくx2+22x+40 = (x )(x )
のところまで書いてしまいましょう。この操作が計算スピードをあげるコツです！
さてそれでは穴埋め問題のように、今空けて書いた部分に値を入れていきます。
x2の項 と 定数項 については展開の際に掛け算をするだけで求められる、ということでしたので、今度は定数項について着目します。
すると空白部分に２つの値を入れることになるのですが、これら２つの値の積は定数項の値(=40)にならなければいけません。
よって空白部分に入る値の候補は、掛け合わせると４０になる値の組です。
実際に探してみると、1 × 40 = 40
2 × 20 = 40
4 × 10 = 40
という候補があがります。この候補を出す際には素因数分解の知識を使うと良いでしょう。４０の素因数分解をしようとすれば自ずと候補の組み合わせが思いつくかと思います。
ではどの候補が正しいのか？という話ですが、これは実際に代入したときの答えと x の係数を比較して下さい。
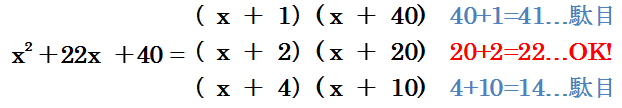今回では(x + …)(x + …)の式を展開した際に x の係数が22にならなければいけないので、そのような答えを考えると右図のように1 + 40 = 41
2 + 20 = 22
4 + 10 = 14
となるので、和が22になっている (x+2)(x+20)が答えだと分かります。この２つの値の和を求める作業ですが、 ２つの値同士が離れているほど和は大きくなるということを意識しておくと今後の学習に役立ちます。
長々とした説明でしたが、結局は
x2+bx+c = (x )(x )
という形が答えになる、ということです。
空白に入る値同士を掛け合わせた値がC,足し合わせた値がｂということに注意して以下の問題に取り組んでみて下さい。
今度は x2-11x+10 の式を因数分解することを考えます。
今回は x の係数の値が負になっていますが、基本的な考え方は先程と何も変わりません。
まず x2 の係数が１であることを考えれば、右図のようにx2-11x+10 = (x )(x )
という形で表記できます。まずはここまで解答用紙に書いてしまいましょう。
次に今までと同様に穴埋め作業に入ります。掛け合わせて１０になる値を考えると1 × 10 = 10
2 × 5 = 10
という２つ候補があがります。
ではどの候補が正しいのか？という話ですが、これは実際に代入したときの答えと x の係数を比較するのでしたね？
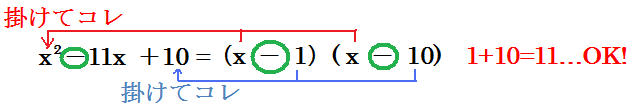ただ一つ注意して欲しいのが、xの係数が負であることです。そうすると「あれ？答えがない？」と思われる方もいると思いますが、掛け合わせて１０になる値というのは実は上の２つ以外にもあるのです。
1 × 10 = 10
(-1) × (-10) = 10
2 × 5 = 10
(-2) × (-5) = 10
このように負の値まで含めて考えると４つの候補がありますね。しかし、結局は上で上がった2つの候補の両方にマイナスを付けただけ、という話です。
なので先ず足して１１になるのは１０と１の組み合わせということに気が付いたら、あとは正負の帳尻を合わせるだけと考えておけば良い、という話です。
以上のプロセスから x2-11x+10 = (x-1)(x-10) が答えだと分かります。
今までの内容を踏まえて以下の問題に取り組んでみて下さい。
今度は x2-18x-40 の式を因数分解することを考えます。
今回は定数項の値が負になっていますが、基本的な考え方は先程と何も変わりません。
まず x2 の係数が１であることを考えれば、右図のようにx2-18x-40 = (x )(x )
という形で表記できます。まずはここまで解答用紙に書いてしまいましょう。
次に今までと同様に穴埋め作業に入りますが定数項の値が負になっています。しかし、この定数項の大きさ40だけに着目してどのような値を掛け合わせれば40に出来るか？について考えてみましょう。[1] 1 × 40 = 40
[2] 2 × 20 = 40
[3] 4 × 10 = 40
という３つの候補があがります。しかしこれは大きさだけに着目した掛け算なので、厳密には先程の問題と同様負の値も用いた掛け算の形で考えるなくてはいけません。
負の値まで含めて考えて、2つの値同士を掛け合わせて-40になるような組み合わせは
[1-1] 1 × (-40) = -40
[1-2] (-1) × 40 = -40
[2-1] 2 × (-20) = -40
[2-2] (-2) × 20 = -40
[3-1] 4 × (-10) = -40
[3-2] (-4) × 10 = -40
という６つの候補があるのです。しかし、最終的に計算する内容を考えるとこれらの値同士を足し合わせて-18になるように値を選ばなければいけません。
いったん上の６つの候補の全ての和をそれぞれ書いてみます。
[1-1] 1 + (-40) = -39
[1-2] (-1) + 40 = 39
[2-1] 2 + (-20) = -18
[2-2] (-2) + 20 = 18
[3-1] 4 + (-10) = -6
[3-2] (-4) + 10 = 6
上の和を見ると分かりますが、代入する２つの値の正負が反転しても、同じ値の組み合わせであれば答えの正負が反転するだけなのです。
なので、重要なのはむしろ代入する２つの値の差になってきます。つまり次の内容です。
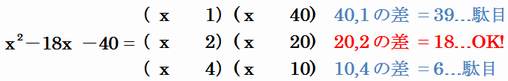[1] 1 と 40 の差は 39[2] 2 と 20 の差は 18
[3] 4 と 10 の差は 6
という様に意識すると良いでしょう。今両者の差は「18」になって欲しいとのことでしたので、次のように
x2-18x-40 = (x 2)(x 20)
という形で表記できます。ですので、ここまで解答用紙に書いてしまいましょう。
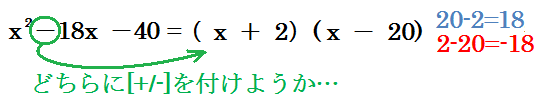あとはどちらにプラス・どちらにマイナスを付ければいいの？という話ですが、これはすぐに分かるのではないでしょうか？今 x の係数は -18 になって欲しいということでしたので、マイナスの値にならなくてはいけないのでしたね？と、いうことはマイナスの値が大きくなるように20の方にマイナスを付ければいいのです。
よって答えは x2-18x-40 = (x + 2)(x - 20) が答えだと分かります。
これで x2+bx+c の形のものの因数分解の方法についての説明は終了いたします。いずれの問題にしても結局は
x2+bx+c = (x )(x )
と書いた後に、残った部分の穴埋めをしよう！という意識でいいのです。
あとは空白に入る値を掛け合わせた値がC,足し合わせた値がｂとなるように正負を考えながら代入する、という意識を持っておけば 問題ありません。実際にやってみると非常に簡単です。あとは問題数をこなして慣れていくことが大切でしょう。
以下に問題を用意したので、練習がてら解いて見て下さい。内容は今回のセクションでのまとめ問題となっています。
とりあえずここまで解いたところで大丈夫でしょうか？次のページからはいよいよ
ax2+bx+c
という一般の形での因数分解について解説いたします。